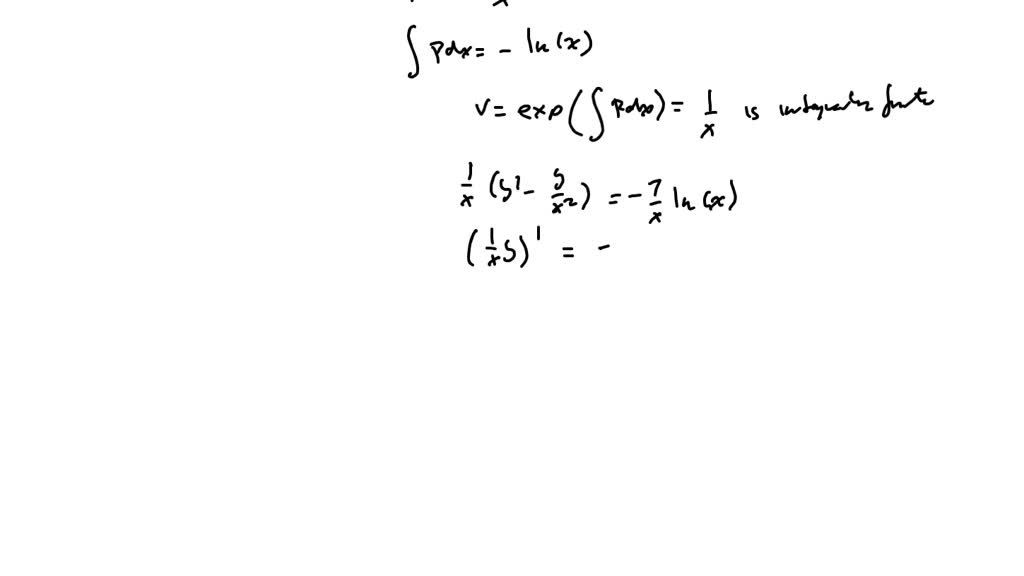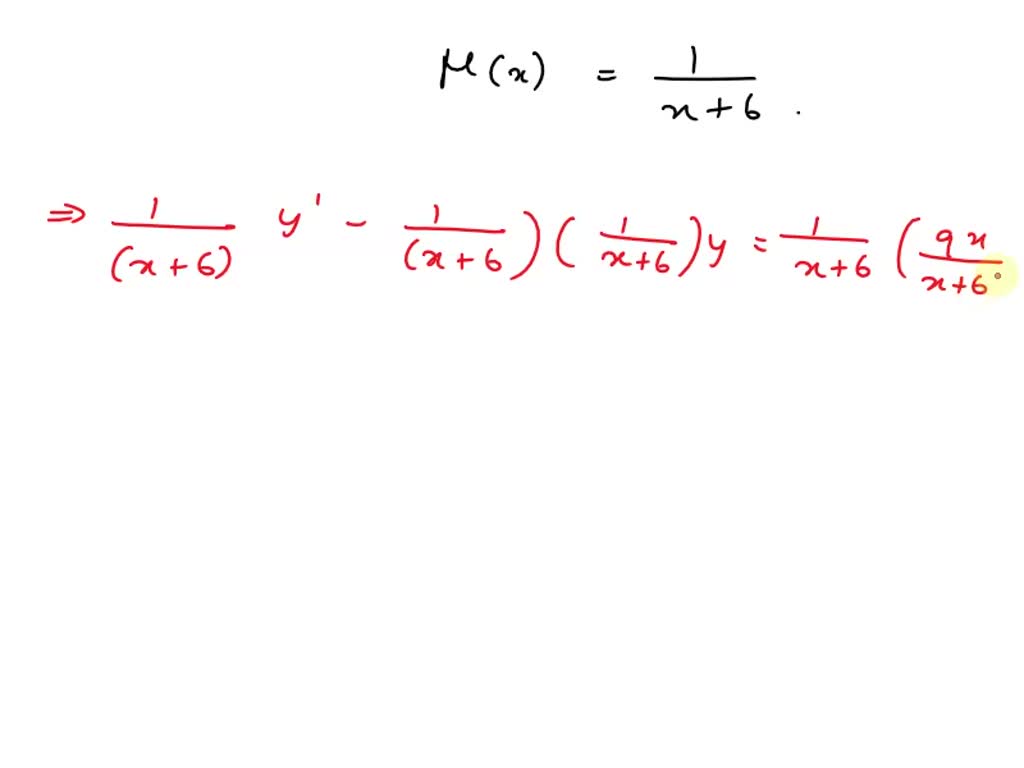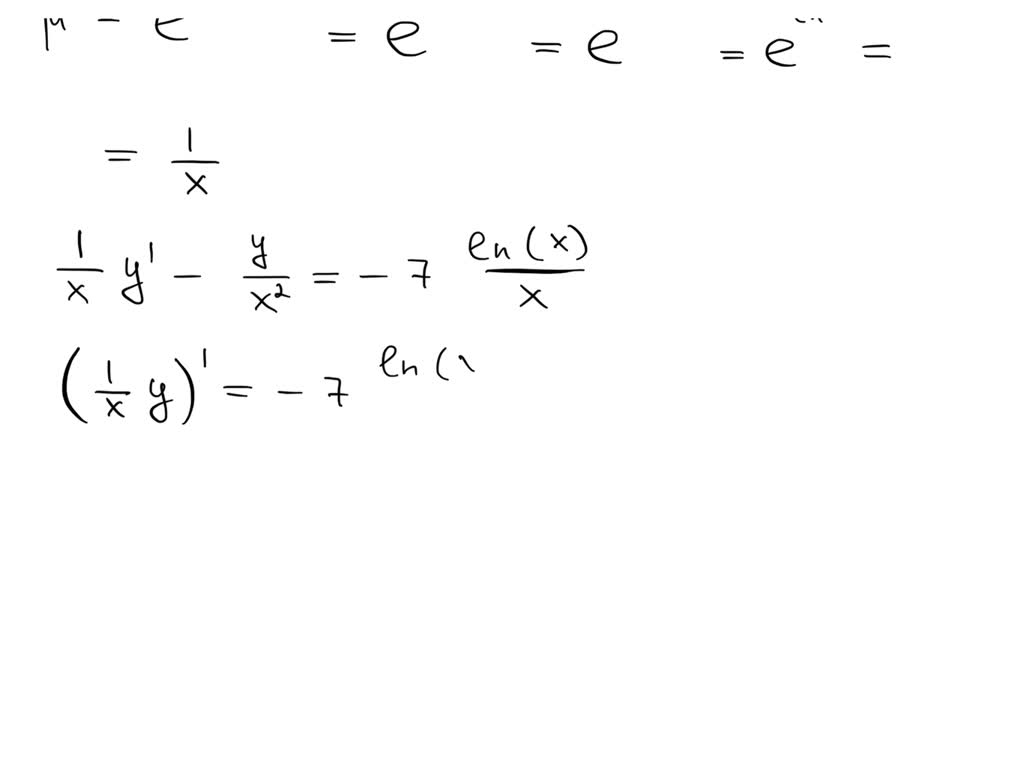Solve The Following Differential Equation By Using Integrating Factors. - Can be solved using the integrating factor method. After writing the equation in standard form, p(x) can be. A linear first order o.d.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
A linear first order o.d.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. After writing the equation in standard form, p(x) can be. Can be solved using the integrating factor method.
A linear first order o.d.e. Can be solved using the integrating factor method. After writing the equation in standard form, p(x) can be. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
Solved By finding an appropriate integrating factor, solve
Can be solved using the integrating factor method. A linear first order o.d.e. After writing the equation in standard form, p(x) can be. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
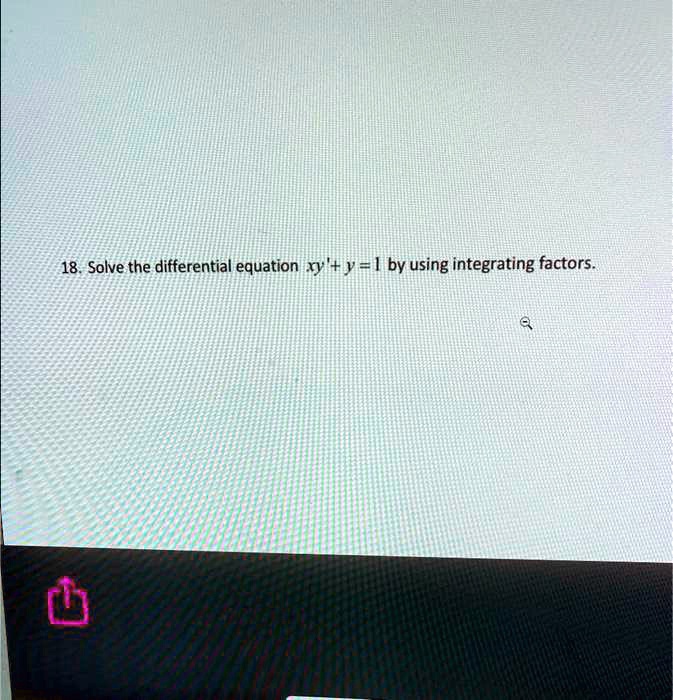
VIDEO solution Solve the differential equation y by using integrating
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Can be solved using the integrating factor method. A linear first order o.d.e. After writing the equation in standard form, p(x) can be.
SOLVED Solve the following differential equation by using integrating
Can be solved using the integrating factor method. A linear first order o.d.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. After writing the equation in standard form, p(x) can be.
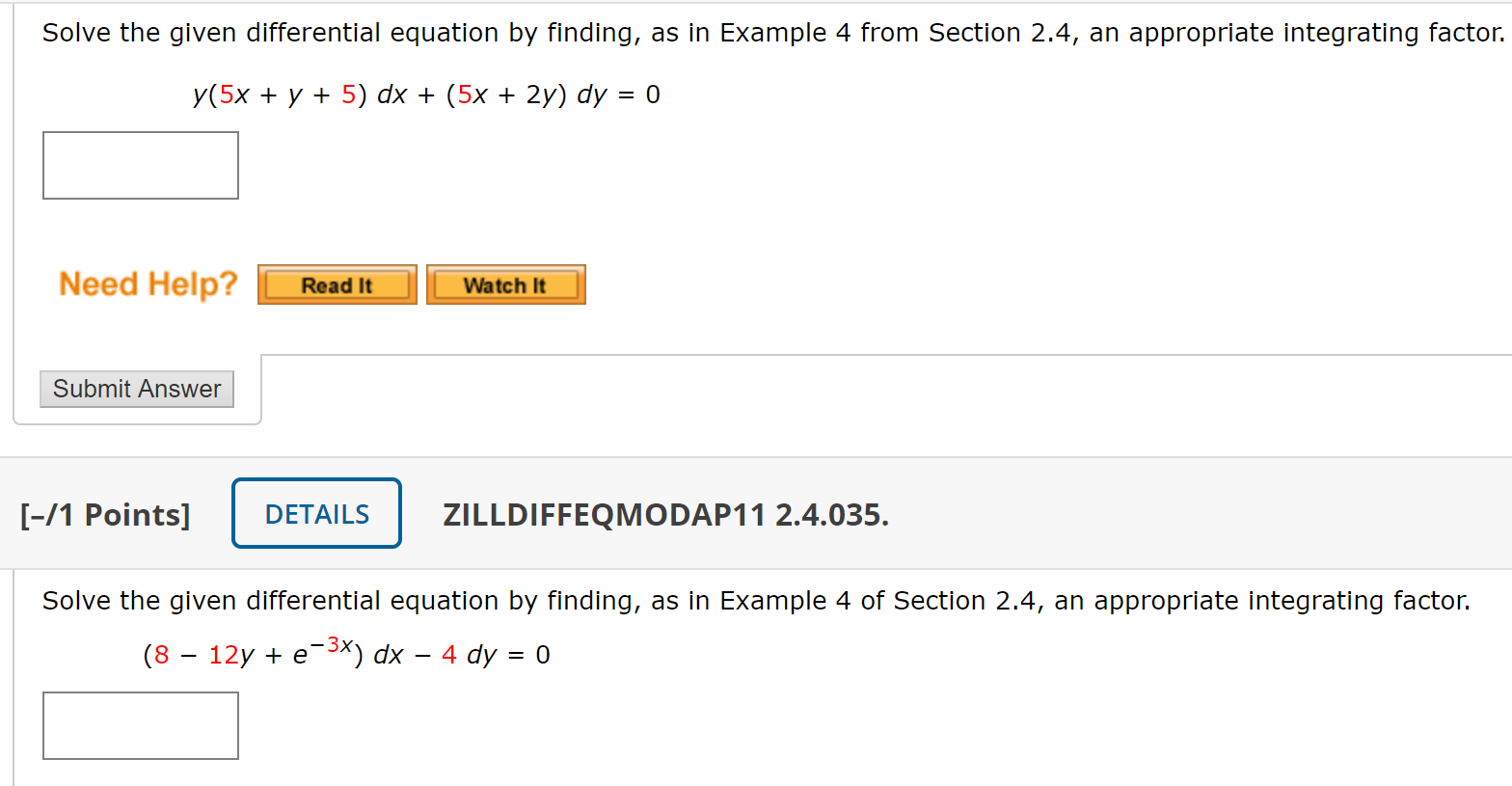
Solved Solve the given differential equation by finding, as
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Can be solved using the integrating factor method. After writing the equation in standard form, p(x) can be. A linear first order o.d.e.
Solved 1. Integrating Factor. Find the general solution to
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. After writing the equation in standard form, p(x) can be. A linear first order o.d.e. Can be solved using the integrating factor method.
integrating factor of the differential equation X dy/dxy = 2 x ^2 is A
Can be solved using the integrating factor method. A linear first order o.d.e. After writing the equation in standard form, p(x) can be. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
Integrating Factor Differential Equation All in one Photos
A linear first order o.d.e. After writing the equation in standard form, p(x) can be. Can be solved using the integrating factor method. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
VIDEO solution Solve the following differential equation by using
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e. After writing the equation in standard form, p(x) can be. Can be solved using the integrating factor method.
Solved Which of the following is the appropriate integrating
A linear first order o.d.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Can be solved using the integrating factor method. After writing the equation in standard form, p(x) can be.
SOLVED Solve the following differential equation by using integrating
Can be solved using the integrating factor method. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e. After writing the equation in standard form, p(x) can be.
After Writing The Equation In Standard Form, P(X) Can Be.
Can be solved using the integrating factor method. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e.