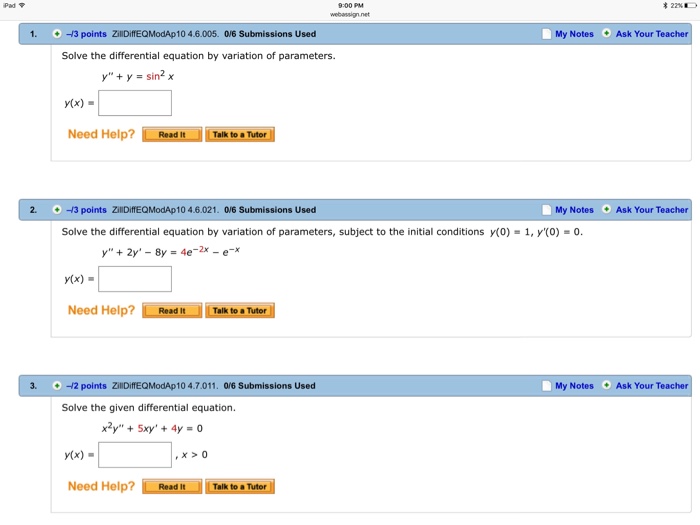
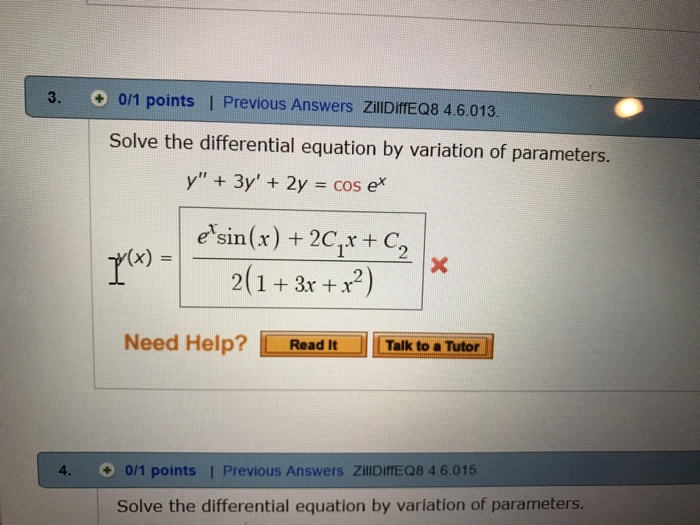
Solve The Given Differential Equation By Variation Of Parameters. - 4.6 variation of parameters 195. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. Continuity of a, b, c. Variation of parameters is a powerful theoretical tool used by researchers in differential equations. The method of variation of parameters applies to solve (1) a(x)y′′+b(x)y′+c(x)y = f(x). In this section we will give a detailed discussion of the process for using variation of parameters for higher order. In order to determine a particular solution of the nonhomogeneous equation, we vary the parameters \(c_{1}\) and \(c_{2}\) in the. We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a.
In order to determine a particular solution of the nonhomogeneous equation, we vary the parameters \(c_{1}\) and \(c_{2}\) in the. Continuity of a, b, c. 4.6 variation of parameters 195. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. The method of variation of parameters applies to solve (1) a(x)y′′+b(x)y′+c(x)y = f(x). We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a. Variation of parameters is a powerful theoretical tool used by researchers in differential equations. In this section we will give a detailed discussion of the process for using variation of parameters for higher order.
In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a. Continuity of a, b, c. In this section we will give a detailed discussion of the process for using variation of parameters for higher order. 4.6 variation of parameters 195. In order to determine a particular solution of the nonhomogeneous equation, we vary the parameters \(c_{1}\) and \(c_{2}\) in the. Variation of parameters is a powerful theoretical tool used by researchers in differential equations. The method of variation of parameters applies to solve (1) a(x)y′′+b(x)y′+c(x)y = f(x).
Solved Solve the differential equation by variation of
In order to determine a particular solution of the nonhomogeneous equation, we vary the parameters \(c_{1}\) and \(c_{2}\) in the. Variation of parameters is a powerful theoretical tool used by researchers in differential equations. Continuity of a, b, c. 4.6 variation of parameters 195. In this section we will give a detailed discussion of the process for using variation of.
Solved Solve the differential equation by variation of
Variation of parameters is a powerful theoretical tool used by researchers in differential equations. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. In this section we will give a detailed discussion of the process for using variation of parameters for higher order. The method of variation of parameters applies to solve.
Solved Solve the differential equation by variation of
In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. Variation of parameters is a powerful theoretical tool used by researchers in differential equations. We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a. In order to determine a particular.
Solved 5 Solve the given differential equation by variation
In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a. 4.6 variation of parameters 195. Continuity of a, b, c. The method of variation of parameters applies to solve (1).
Answered Solve the differential equation by… bartleby
The method of variation of parameters applies to solve (1) a(x)y′′+b(x)y′+c(x)y = f(x). 4.6 variation of parameters 195. In order to determine a particular solution of the nonhomogeneous equation, we vary the parameters \(c_{1}\) and \(c_{2}\) in the. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. Continuity of a, b, c.
Solved Example (Variation of Parameters) Use variation of
The method of variation of parameters applies to solve (1) a(x)y′′+b(x)y′+c(x)y = f(x). Continuity of a, b, c. In this section we will give a detailed discussion of the process for using variation of parameters for higher order. In order to determine a particular solution of the nonhomogeneous equation, we vary the parameters \(c_{1}\) and \(c_{2}\) in the. In this.
Solved In Problems 32 ,solve the given
We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a. In this section we will give a detailed discussion of the process for using variation of parameters for higher order. 4.6 variation of parameters 195. Continuity of a, b, c. The method of variation of parameters applies.
Solved Solve the given thirdorder differential equation by
Continuity of a, b, c. The method of variation of parameters applies to solve (1) a(x)y′′+b(x)y′+c(x)y = f(x). We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a. 4.6 variation of parameters 195. In this section we will give a detailed discussion of the process for using.
Solved 4. Solve each differential equation by variation of
Variation of parameters is a powerful theoretical tool used by researchers in differential equations. Continuity of a, b, c. The method of variation of parameters applies to solve (1) a(x)y′′+b(x)y′+c(x)y = f(x). 4.6 variation of parameters 195. We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a.
[Solved] Solve the given differential equation by variation of
4.6 variation of parameters 195. The method of variation of parameters applies to solve (1) a(x)y′′+b(x)y′+c(x)y = f(x). Variation of parameters is a powerful theoretical tool used by researchers in differential equations. We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a. In order to determine a.
The Method Of Variation Of Parameters Applies To Solve (1) A(X)Y′′+B(X)Y′+C(X)Y = F(X).
Variation of parameters is a powerful theoretical tool used by researchers in differential equations. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. In this section we will give a detailed discussion of the process for using variation of parameters for higher order. 4.6 variation of parameters 195.
In Order To Determine A Particular Solution Of The Nonhomogeneous Equation, We Vary The Parameters \(C_{1}\) And \(C_{2}\) In The.
We’ll show how to use the method of variation of parameters to find a particular solution of \(ly=f\), provided that we know a. Continuity of a, b, c.