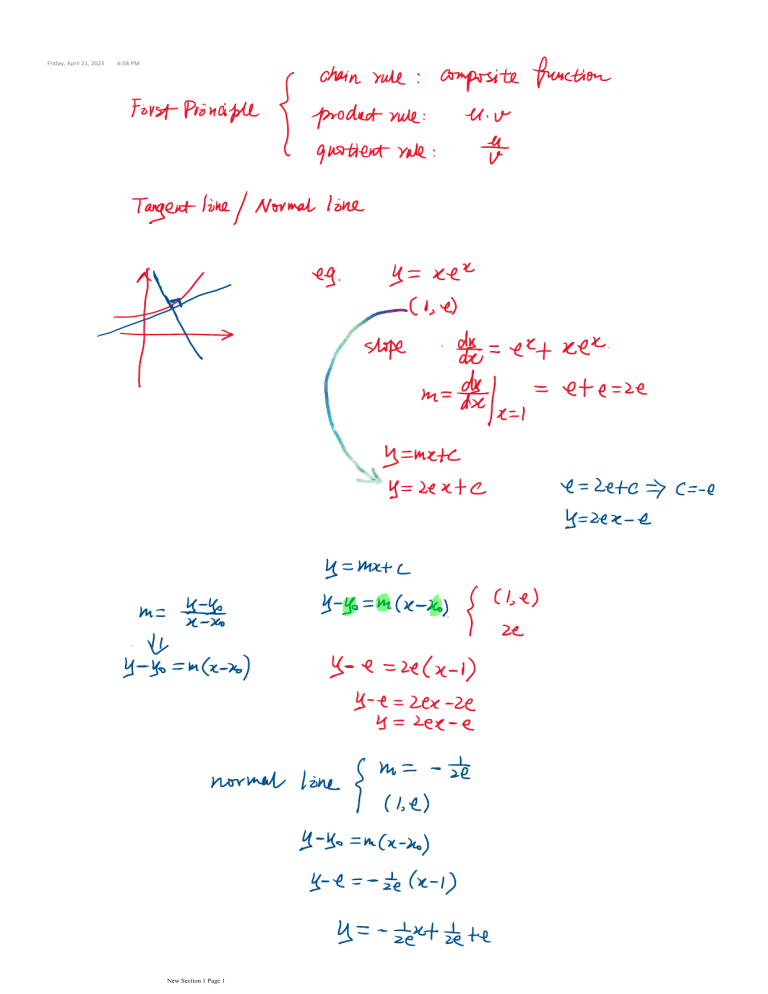
Applications Of Differentiation - To determine whether a point is a maximum or a minimum point or inflexion point, we must. Learn how to use derivatives to find rates of change, critical points, extrema, shapes. In this chapter we look at how derivatives are used to find maximum and minimum values of.
To determine whether a point is a maximum or a minimum point or inflexion point, we must. In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.
To determine whether a point is a maximum or a minimum point or inflexion point, we must. In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.
Applications of Differentiation
In this chapter we look at how derivatives are used to find maximum and minimum values of. To determine whether a point is a maximum or a minimum point or inflexion point, we must. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.
SOLUTION Applications of differentiation Studypool
In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes. To determine whether a point is a maximum or a minimum point or inflexion point, we must.
SOLUTION Differentiation with applications Studypool
To determine whether a point is a maximum or a minimum point or inflexion point, we must. In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.
Applications of Differentiation
Learn how to use derivatives to find rates of change, critical points, extrema, shapes. In this chapter we look at how derivatives are used to find maximum and minimum values of. To determine whether a point is a maximum or a minimum point or inflexion point, we must.
PPT Chapter 3 Applications of Differentiation PowerPoint
In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes. To determine whether a point is a maximum or a minimum point or inflexion point, we must.
SOLUTION Applications of differentiation Studypool
In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes. To determine whether a point is a maximum or a minimum point or inflexion point, we must.
Applications of Differentiation PDF
In this chapter we look at how derivatives are used to find maximum and minimum values of. To determine whether a point is a maximum or a minimum point or inflexion point, we must. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.
Applications of Differentiation 1 PDF
To determine whether a point is a maximum or a minimum point or inflexion point, we must. In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.
SOLUTION Differentiation applications Studypool
To determine whether a point is a maximum or a minimum point or inflexion point, we must. In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.
applications of differentiation notes21042023 (1)
To determine whether a point is a maximum or a minimum point or inflexion point, we must. In this chapter we look at how derivatives are used to find maximum and minimum values of. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.
In This Chapter We Look At How Derivatives Are Used To Find Maximum And Minimum Values Of.
To determine whether a point is a maximum or a minimum point or inflexion point, we must. Learn how to use derivatives to find rates of change, critical points, extrema, shapes.