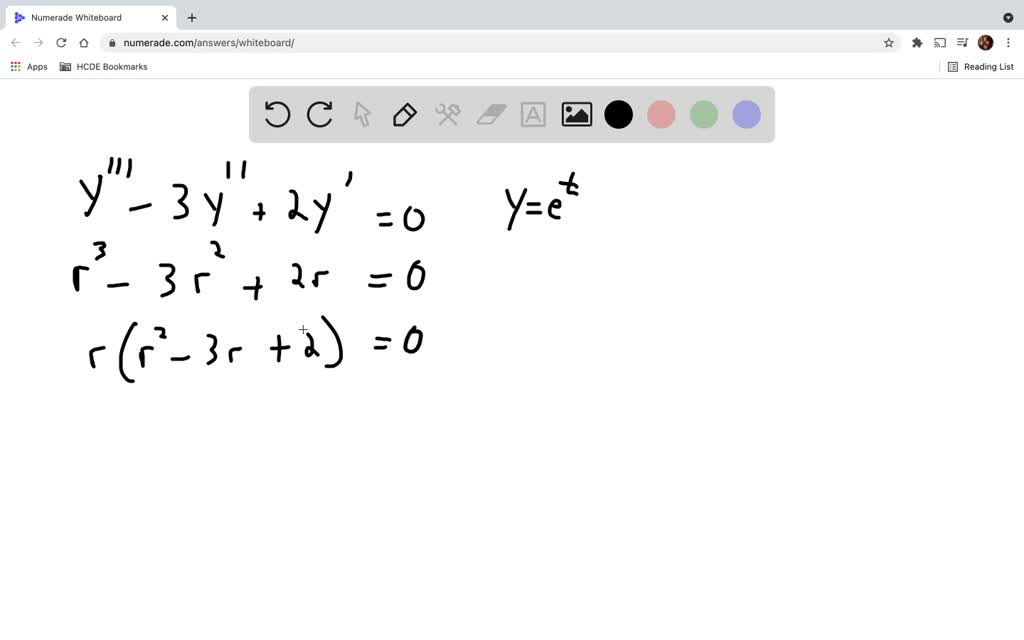
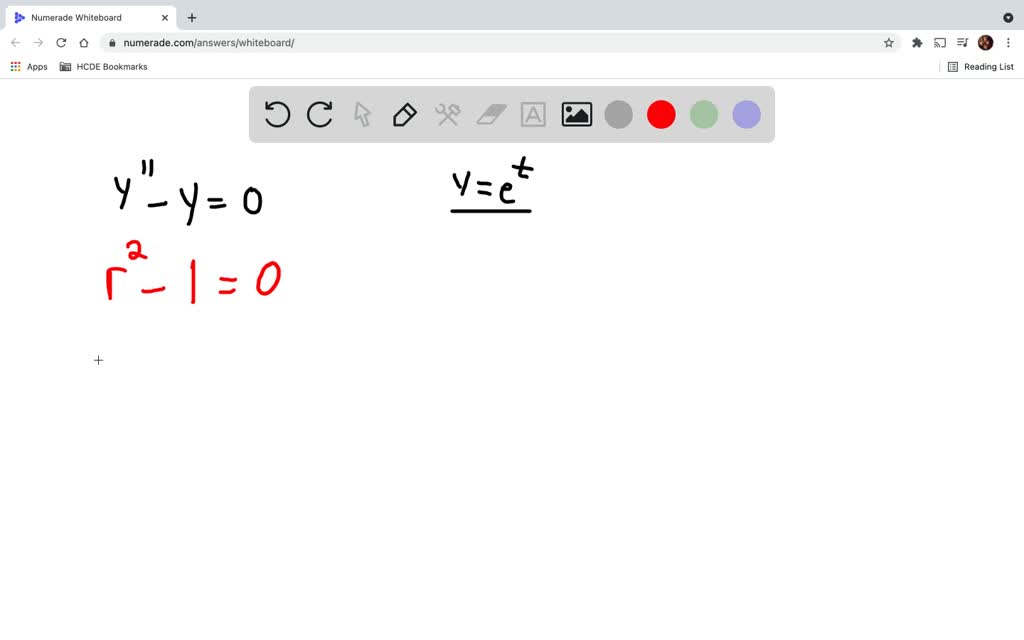
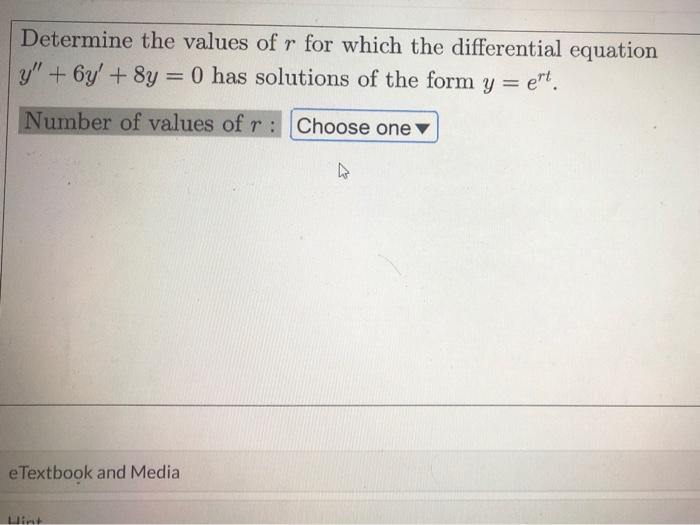
Determine The Values Of R For Which The Differential Equation - Therefore, the values of r for which the given differential equation has solutions of the form y =. Here’s the best way to solve it. The typical form of a characteristic. In each of problems 15 through 18, determine the values of r for which the given differential. The polynomial's roots are the values of r that you're trying to find. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential.
The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. The polynomial's roots are the values of r that you're trying to find. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. In each of problems 15 through 18, determine the values of r for which the given differential. Therefore, the values of r for which the given differential equation has solutions of the form y =. In each of problems 15 through 18, determine the values of r for which the given differential. The typical form of a characteristic. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. In each of problems 15 through 18, determine the values of r for which the given differential. Here’s the best way to solve it.
In each of problems 15 through 18, determine the values of r for which the given differential. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. The typical form of a characteristic. Here’s the best way to solve it. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. In each of problems 15 through 18, determine the values of r for which the given differential. Therefore, the values of r for which the given differential equation has solutions of the form y =. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. In each of problems 15 through 18, determine the values of r for which the given differential. The polynomial's roots are the values of r that you're trying to find.
[Solved] solve the following differential equation, and determine the
Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. In each of problems 15 through 18, determine the values of r for which the given differential. The typical form of a characteristic. Therefore, the values of r for which the given differential equation has solutions of the form y =. Here’s.
Differential Equations (Definition, Types, Order, Degree, Examples)
In each of problems 15 through 18, determine the values of r for which the given differential. Here’s the best way to solve it. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$.
[Solved] Determine singular points, of each differential equation and
The polynomial's roots are the values of r that you're trying to find. In each of problems 15 through 18, determine the values of r for which the given differential. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. In each of problems 15 through 18, determine the values of.
![[Solved] 1. Determine the order of the given differential](https://media.cheggcdn.com/media/2b4/2b49d74b-7985-4a4f-907f-175a8ca9edd8/phplYmz0k)
[Solved] 1. Determine the order of the given differential
In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. The polynomial's roots are the values of r.
[Solved] . Determine whether the given differential equation is exact
Here’s the best way to solve it. In each of problems 15 through 18, determine the values of r for which the given differential. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. Therefore, the values of r for which the given differential equation has solutions of the form y =..
SOLVEDDetermine the values of r for which the given differential
Therefore, the values of r for which the given differential equation has solutions of the form y =. The polynomial's roots are the values of r that you're trying to find. In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r.
Determine the values of r for which the given differential equation has
Therefore, the values of r for which the given differential equation has solutions of the form y =. In each of problems 15 through 18, determine the values of r for which the given differential. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. Here’s the best way to solve.
[Solved] DIFFERENTIAL EQUATIONS. Determine the given differential
In each of problems 15 through 18, determine the values of r for which the given differential. Therefore, the values of r for which the given differential equation has solutions of the form y =. In each of problems 15 through 18, determine the values of r for which the given differential. Here’s the best way to solve it. If.
Differential equation r/maths
In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. Here’s the best way to solve.
Determine The Values Of R For Which The Differential Equation
If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. The typical form of a characteristic. In each of problems 15 through 18, determine the values of r for which the given differential. Therefore, the values of r for which the given differential equation has solutions of the form y.
In Each Of Problems 15 Through 18, Determine The Values Of R For Which The Given Differential.
Therefore, the values of r for which the given differential equation has solutions of the form y =. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. The typical form of a characteristic. Here’s the best way to solve it.
In Each Of Problems 15 Through 18, Determine The Values Of R For Which The Given Differential.
The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. The polynomial's roots are the values of r that you're trying to find. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. In each of problems 15 through 18, determine the values of r for which the given differential.