Differential Of Integral - As stated above, the basic differentiation rule for integrals is: Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. $\ \ \ \ \ \ $for $f(x)=\int_a^x f. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite.
Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. $\ \ \ \ \ \ $for $f(x)=\int_a^x f. As stated above, the basic differentiation rule for integrals is: Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals.
$\ \ \ \ \ \ $for $f(x)=\int_a^x f. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. As stated above, the basic differentiation rule for integrals is: Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals.
SOLUTION Differential and integral calculus Studypool
Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. As stated above, the basic differentiation rule for integrals is: $\ \ \ \ \ \ $for $f(x)=\int_a^x f. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite.
Rules Of Differential & Integral Calculus.
Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. $\ \ \ \ \ \ $for $f(x)=\int_a^x f. As stated above, the basic differentiation rule for integrals is: Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals.
DIFFERENTIAL and INTEGRAL CALCULUS Shopee Philippines
Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. $\ \ \ \ \ \ $for $f(x)=\int_a^x f. As stated above, the basic differentiation rule for integrals is: Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals.
Mathematics Lesson Differential and Integral Calculus Chalkboard. Stock
As stated above, the basic differentiation rule for integrals is: Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. $\ \ \ \ \ \ $for $f(x)=\int_a^x f.
Differential integral calculus hires stock photography and images Alamy
$\ \ \ \ \ \ $for $f(x)=\int_a^x f. As stated above, the basic differentiation rule for integrals is: Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite.
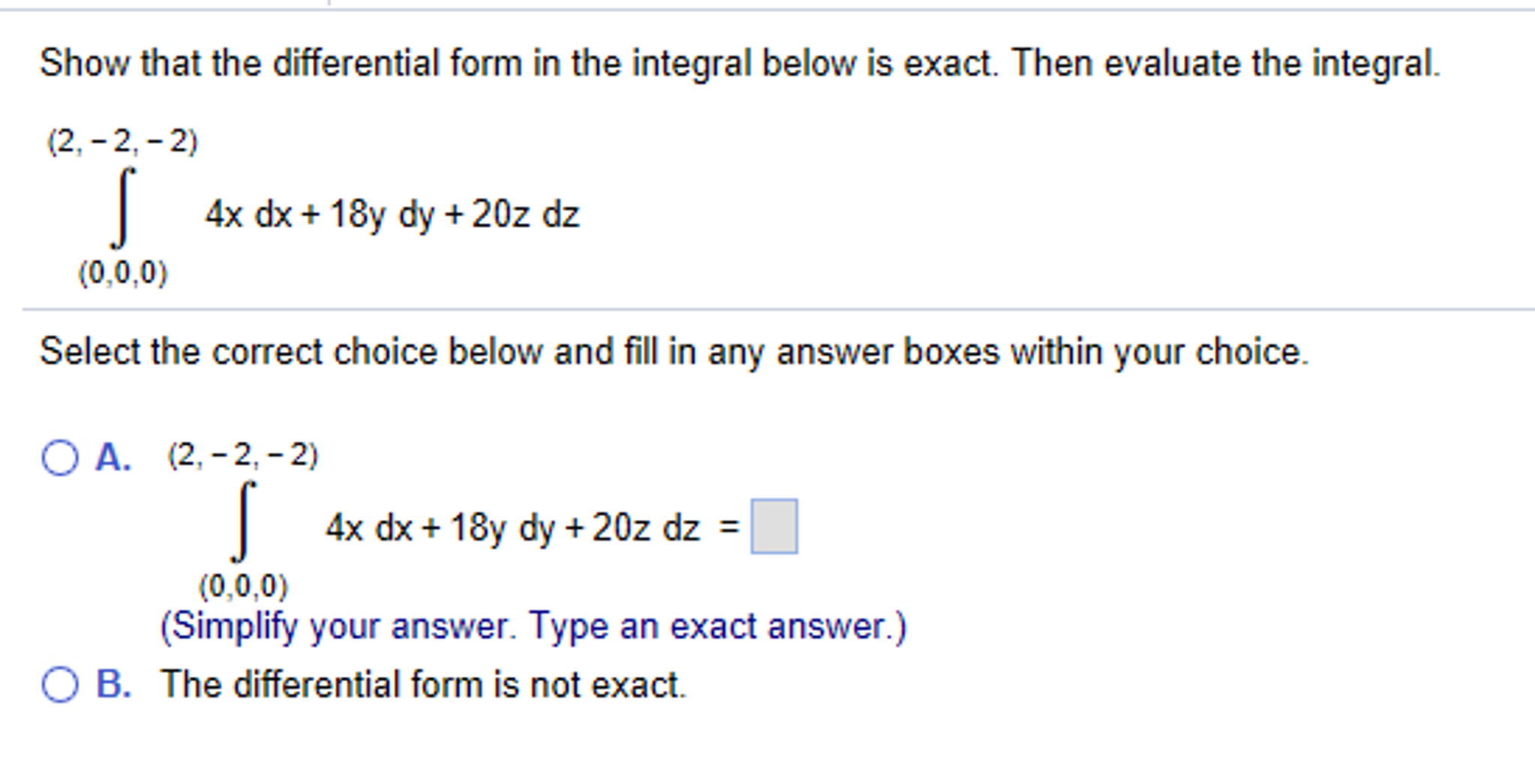
Solved Show that the differential form in the integral below
$\ \ \ \ \ \ $for $f(x)=\int_a^x f. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. As stated above, the basic differentiation rule for integrals is: Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals.
Differential Integral Calculus PDF
Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. $\ \ \ \ \ \ $for $f(x)=\int_a^x f. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. As stated above, the basic differentiation rule for integrals is:
DIFFERENTIAL AND INTEGRAL CALCULUS Lazada PH
$\ \ \ \ \ \ $for $f(x)=\int_a^x f. As stated above, the basic differentiation rule for integrals is: Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals.
Differential & Integral Calculus R. Courant Free Download, Borrow
As stated above, the basic differentiation rule for integrals is: Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. $\ \ \ \ \ \ $for $f(x)=\int_a^x f.
SOLUTION Differential and integral calculus formula Studypool
Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite. As stated above, the basic differentiation rule for integrals is: $\ \ \ \ \ \ $for $f(x)=\int_a^x f.
Unless The Variable X Appears In Either (Or Both) Of The Limits Of Integration, The Result Of The Definite.
As stated above, the basic differentiation rule for integrals is: Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. $\ \ \ \ \ \ $for $f(x)=\int_a^x f.