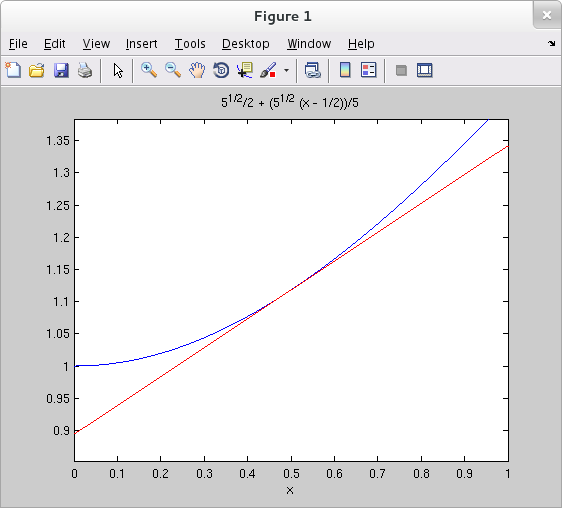
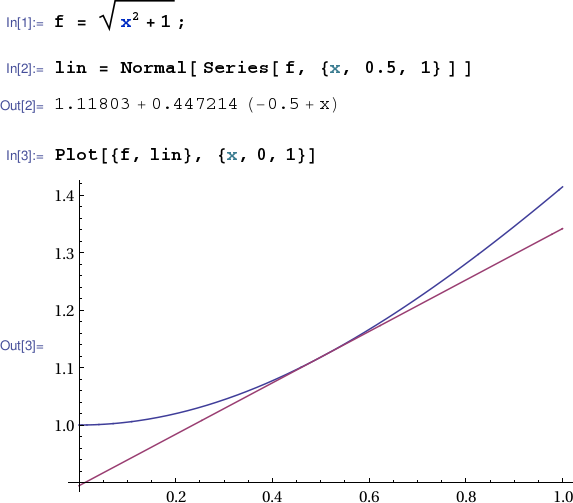
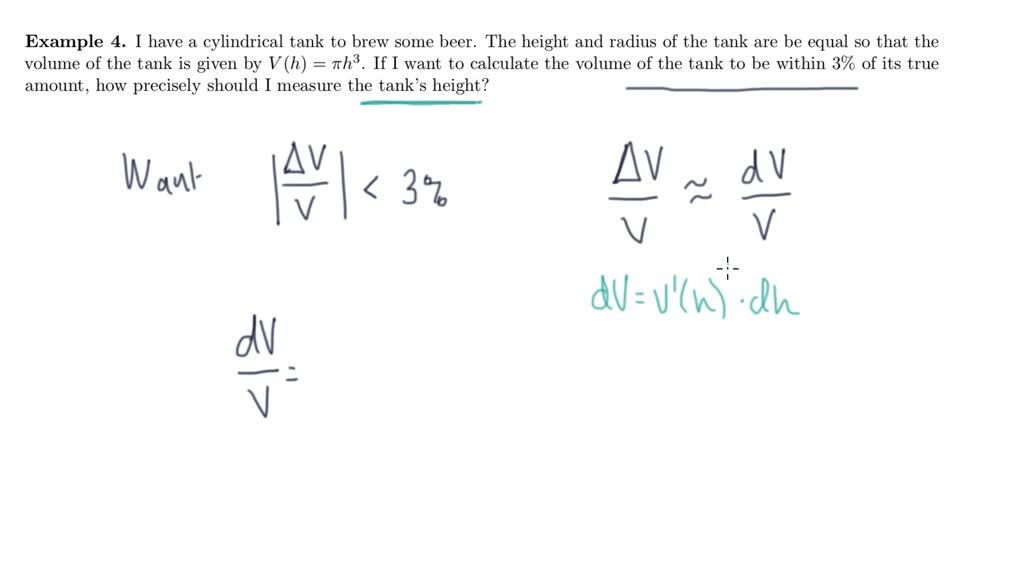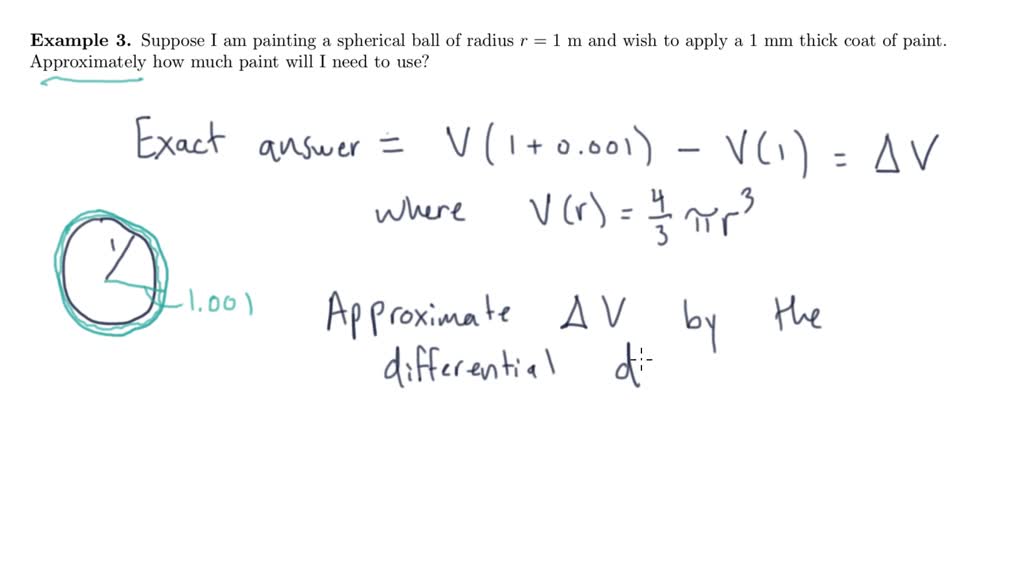Differentials And Linearization - 3.11 linearization and differentials 4 definition. This calculus video tutorial provides a basic introduction into differentials and. Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. We have seen that linear approximations can be used to estimate function. We can compare actual changes in a function and the. What does it mean for a function of two variables to be locally linear at a point? In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with.
What does it mean for a function of two variables to be locally linear at a point? Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. We can compare actual changes in a function and the. In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with. 3.11 linearization and differentials 4 definition. This calculus video tutorial provides a basic introduction into differentials and. We have seen that linear approximations can be used to estimate function.
In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with. 3.11 linearization and differentials 4 definition. Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. We have seen that linear approximations can be used to estimate function. We can compare actual changes in a function and the. What does it mean for a function of two variables to be locally linear at a point? This calculus video tutorial provides a basic introduction into differentials and.
3.9 Linearization and Differentials
This calculus video tutorial provides a basic introduction into differentials and. In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with. We can compare actual changes in a function and the. We have seen that linear approximations can be used to estimate function. 3.11 linearization and differentials 4 definition.
WS 03.7 Linearization & Differentials KEY PDF
Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. We can compare actual changes in a function and the. We have seen that linear approximations can be used to estimate function. In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with. 3.11 linearization and differentials 4 definition.
3.9 Linearization and Differentials
What does it mean for a function of two variables to be locally linear at a point? We have seen that linear approximations can be used to estimate function. Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with..
Linearization and differentials example 1 Numerade
Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with. We can compare actual changes in a function and the. What does it mean for a function of two variables to be locally linear at a point? This calculus.
Linearization and Differentials
3.11 linearization and differentials 4 definition. We have seen that linear approximations can be used to estimate function. Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with. We can compare actual changes in a function and the.
Linearization and differentials overview Numerade
This calculus video tutorial provides a basic introduction into differentials and. We have seen that linear approximations can be used to estimate function. We can compare actual changes in a function and the. 3.11 linearization and differentials 4 definition. Example 1 find the linearization l(x) of the function f(x) = sinxat π/6.
(PDF) SECTION 3.5 DIFFERENTIALS and LINEARIZATION OF FUNCTIONSkkuniyuk
Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. What does it mean for a function of two variables to be locally linear at a point? We have seen that linear approximations can be used to estimate function. 3.11 linearization and differentials 4 definition. We can compare actual changes in a function and the.
Linearization and differentials overview Numerade
Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. We can compare actual changes in a function and the. This calculus video tutorial provides a basic introduction into differentials and. What does it mean for a function of two variables to be locally linear at a point? In calculus, the differential represents the principal part of.
(PDF) SECTION 3.5 DIFFERENTIALS and LINEARIZATION OF FUNCTIONSkkuniyuk
In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with. 3.11 linearization and differentials 4 definition. Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. This calculus video tutorial provides a basic introduction into differentials and. We can compare actual changes in a function and the.
Linearization and differentials overview Numerade
We can compare actual changes in a function and the. Example 1 find the linearization l(x) of the function f(x) = sinxat π/6. 3.11 linearization and differentials 4 definition. This calculus video tutorial provides a basic introduction into differentials and. In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with.
What Does It Mean For A Function Of Two Variables To Be Locally Linear At A Point?
This calculus video tutorial provides a basic introduction into differentials and. We can compare actual changes in a function and the. In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with. We have seen that linear approximations can be used to estimate function.
3.11 Linearization And Differentials 4 Definition.
Example 1 find the linearization l(x) of the function f(x) = sinxat π/6.