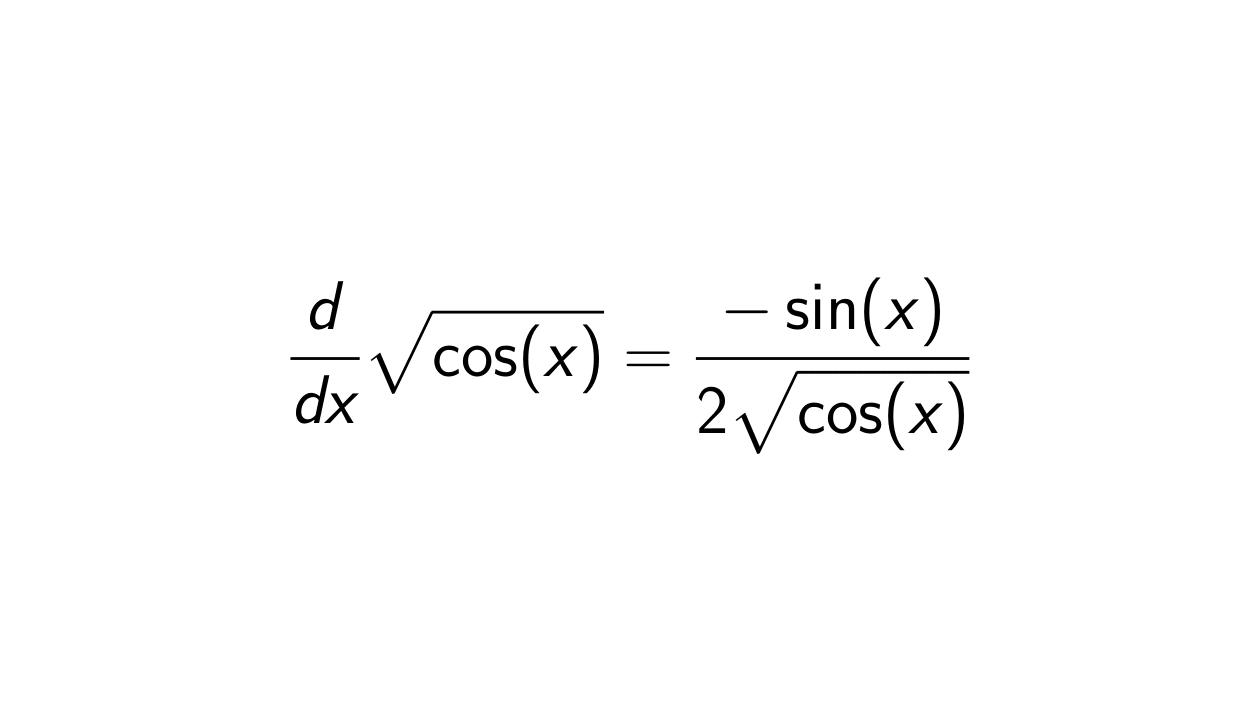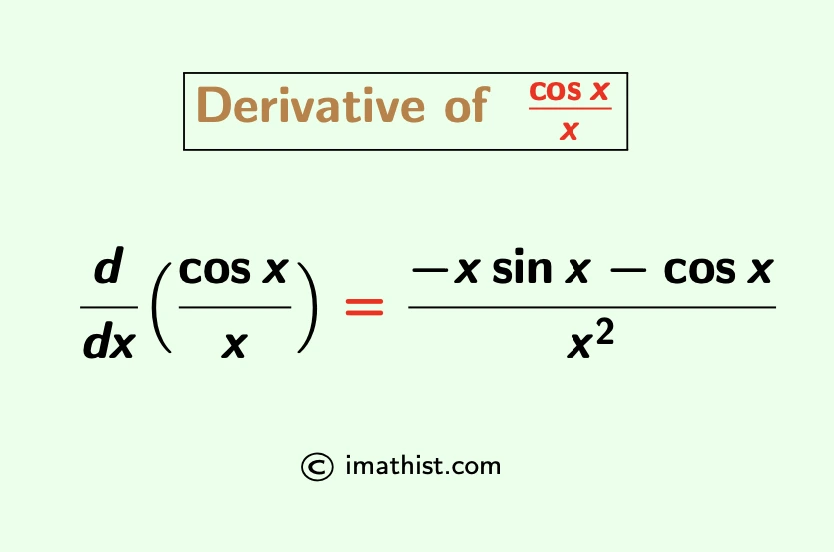Differentiate Cosx - Using the definition of a derivative: We substitute in our function to get: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx.
We substitute in our function to get: Using the definition of a derivative: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx.
Using the definition of a derivative: We substitute in our function to get: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx.
Derivative of square root cos(x) Detailed Solution Epsilonify
Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx. We substitute in our function to get: Using the definition of a derivative:
Solved Differentiate Y = (cos X)^2^x Y' = 2^x(cos X)^2^x
We substitute in our function to get: Using the definition of a derivative: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx.
Derivative of cosx/x (cosx divided by x) iMath
Using the definition of a derivative: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx. We substitute in our function to get:
differentiate x2 cosx from first principle Maths Limits and
We substitute in our function to get: Using the definition of a derivative: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx.
Ex 5.5, 10 Differentiate x^(x cos x) + (x^2 + 1)/(x^2 1)
Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx. Using the definition of a derivative: We substitute in our function to get:
Ex 5.5, 10 Differentiate x^(x cos x) + (x^2 + 1)/(x^2 1)
Using the definition of a derivative: We substitute in our function to get: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx.
35. Differentiate "cosx" with respect to x from first principles.36. Ver..
We substitute in our function to get: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx. Using the definition of a derivative:
differentiate cosx^sinx w.r.t x
We substitute in our function to get: Using the definition of a derivative: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx.
Differentiating f(x)=cosx Using a Specific Rule Calculus
Using the definition of a derivative: We substitute in our function to get: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx.
Ex 5.7, 3 Find second order derivatives of x cosx Ex 5.7
Using the definition of a derivative: Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx. We substitute in our function to get:
Using The Definition Of A Derivative:
Dy dx = lim h→0 f (x + h) − f (x) h, where h = δx. We substitute in our function to get: