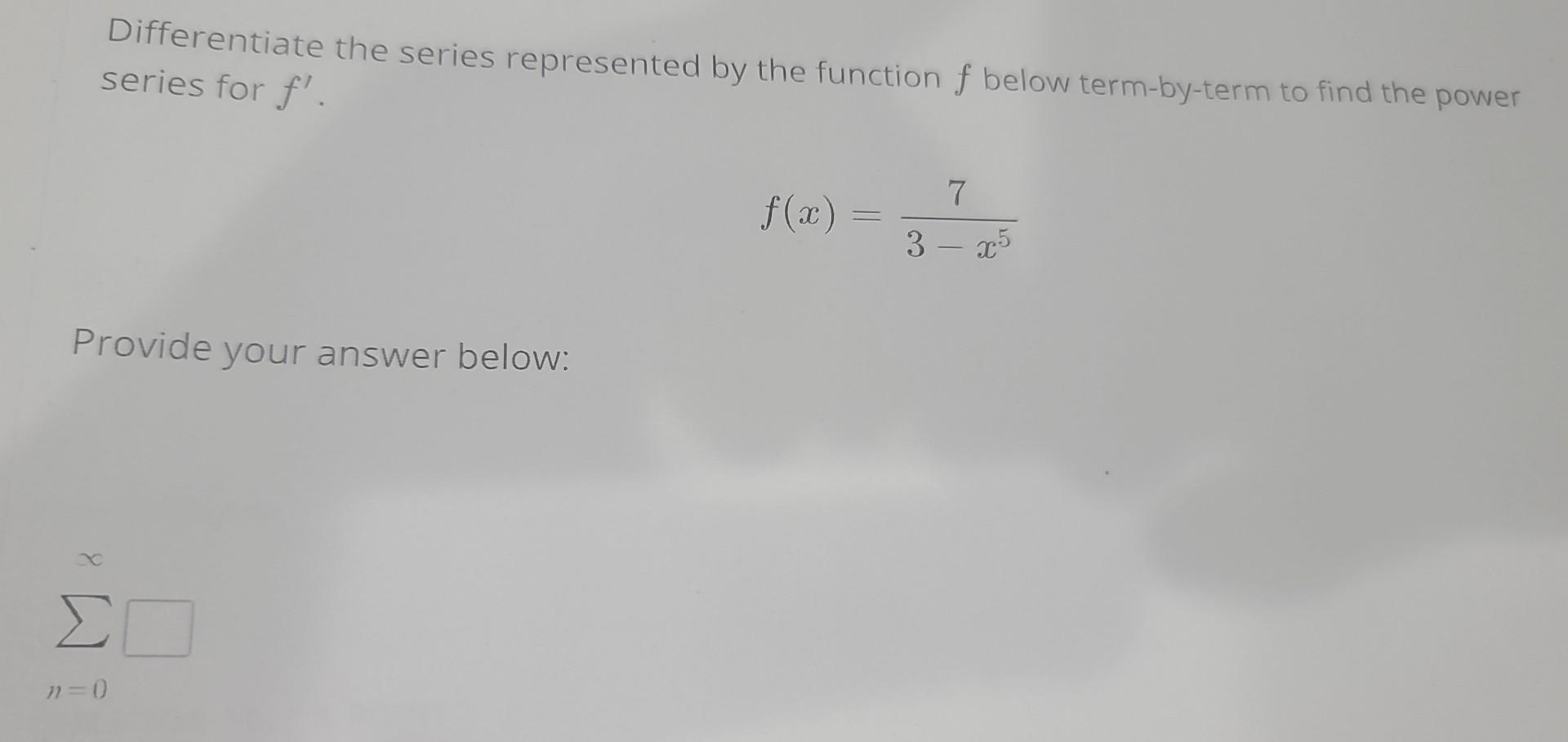Differentiate Power Series - Just recall that a power series is the taylor. Combine power series by addition or subtraction. Create a new power series by multiplication by a power of the variable or a. If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: Differentiation of power series strategy: To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into summation.
Just recall that a power series is the taylor. If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: Combine power series by addition or subtraction. Create a new power series by multiplication by a power of the variable or a. Differentiation of power series strategy: To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into summation.
Differentiation of power series strategy: Create a new power series by multiplication by a power of the variable or a. If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into summation. If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: Just recall that a power series is the taylor. Combine power series by addition or subtraction.
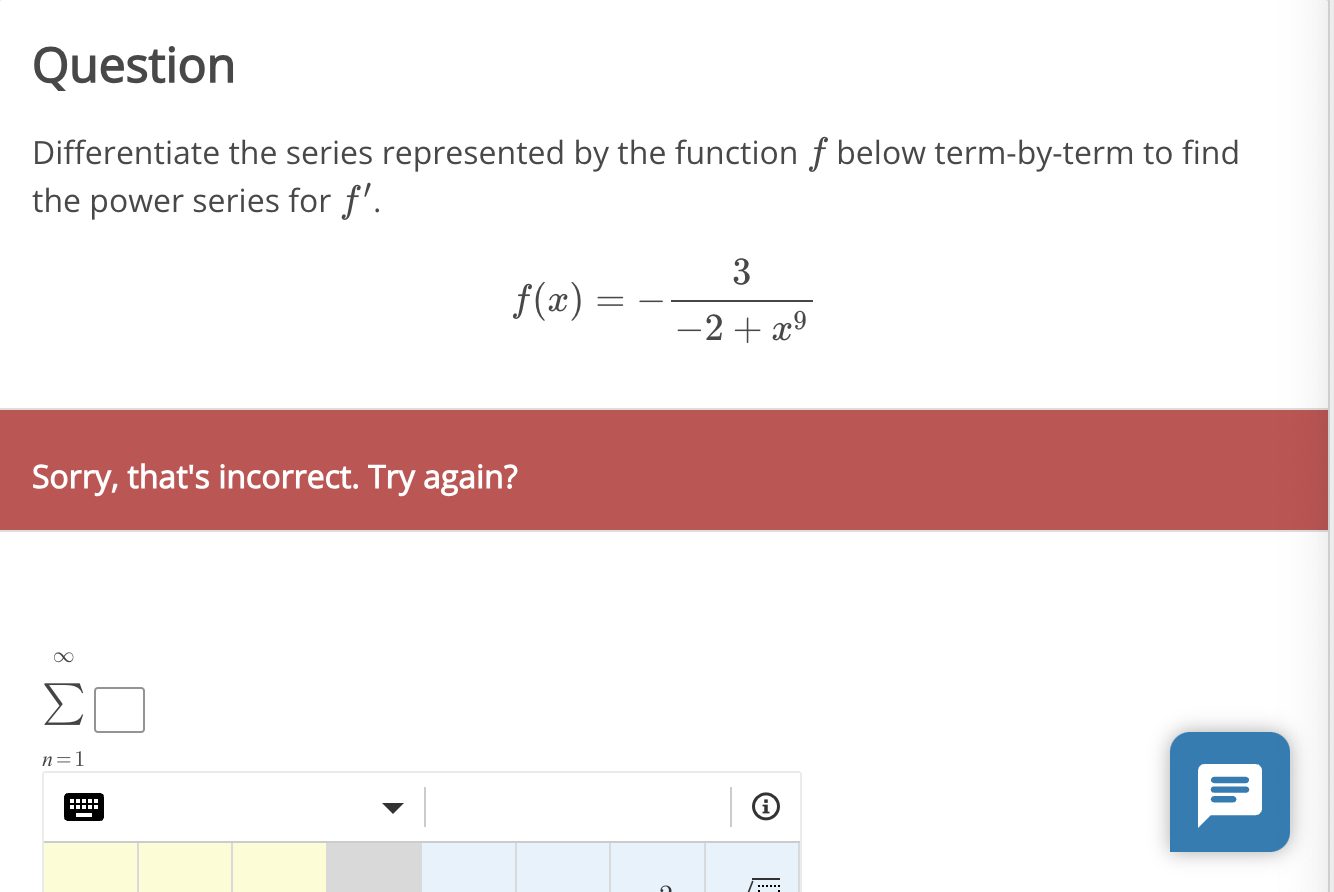
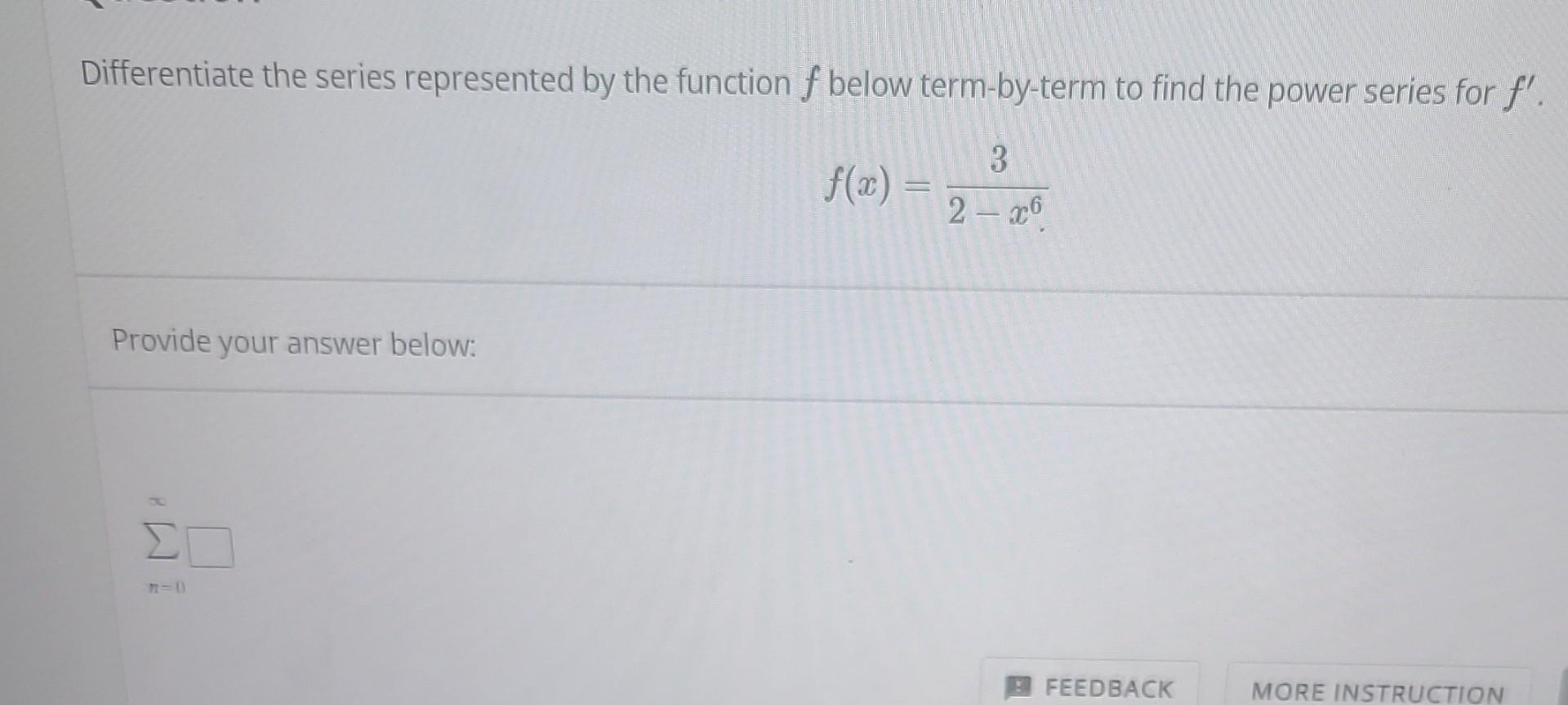
Solved Differentiate the series represented by the function
Differentiation of power series strategy: If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: Just recall that a power series is the taylor. To differentiate, we simply differentiate each.
Solved Differentiate the power series representation of
Just recall that a power series is the taylor. To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into summation. Differentiation of power series strategy: If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: Create a new power series.
3 Power Series PDF PDF Power Series Ordinary Differential Equation
Differentiation of power series strategy: If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: Create a new power series by multiplication by a power of the variable or a..
Power Series PDF
If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: Create a new power series by multiplication by a power of the variable or a. To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into summation. Combine power series by.
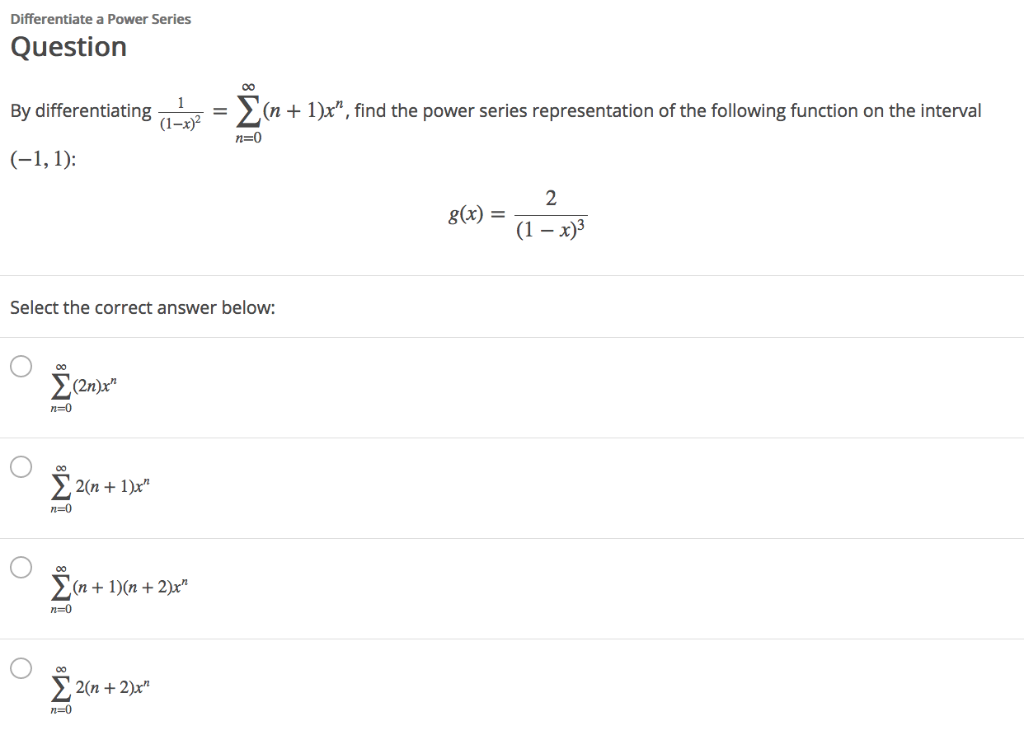
Solved Differentiate a Power Series Question By
If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. Combine power series by addition or subtraction. If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: To differentiate, we simply differentiate each term (not worrying that we have infinitely.
Solved Differentiate the series represented by the function
If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. Combine power series by addition or subtraction. Just recall that a power series is the taylor. To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into.
Power Series PDF
If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: Just recall that a power series is the taylor. If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. Create a new power series by multiplication by a power of.
[Solved] Differentiate power series. Question Differentiate the series
To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into summation. If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. Just recall that a power series is the taylor. If your task is to compute.
Solved Differentiate the series represented by the function
If your task is to compute the second derivative at $x=0$, you don't need to differentiate the series: To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into summation. If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series.
Power Series Representations of Functions Techniques for Finding
If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of. To differentiate, we simply differentiate each term (not worrying that we have infinitely many terms) and then put the terms back into summation. Differentiation of power series strategy: Combine power series by addition or subtraction. If your task.
To Differentiate, We Simply Differentiate Each Term (Not Worrying That We Have Infinitely Many Terms) And Then Put The Terms Back Into Summation.
Create a new power series by multiplication by a power of the variable or a. Combine power series by addition or subtraction. Just recall that a power series is the taylor. If we have a function f(x) = x1 n=0 a n(x a)n that is represented by a power series with radius of.
If Your Task Is To Compute The Second Derivative At $X=0$, You Don't Need To Differentiate The Series:
Differentiation of power series strategy: