Differentiating A Matrix - It will always work to. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Review of multivariate differentiation, integration, and optimization, with applications to data science.
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Review of multivariate differentiation, integration, and optimization, with applications to data science. It will always work to. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors?
Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. It will always work to. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column.
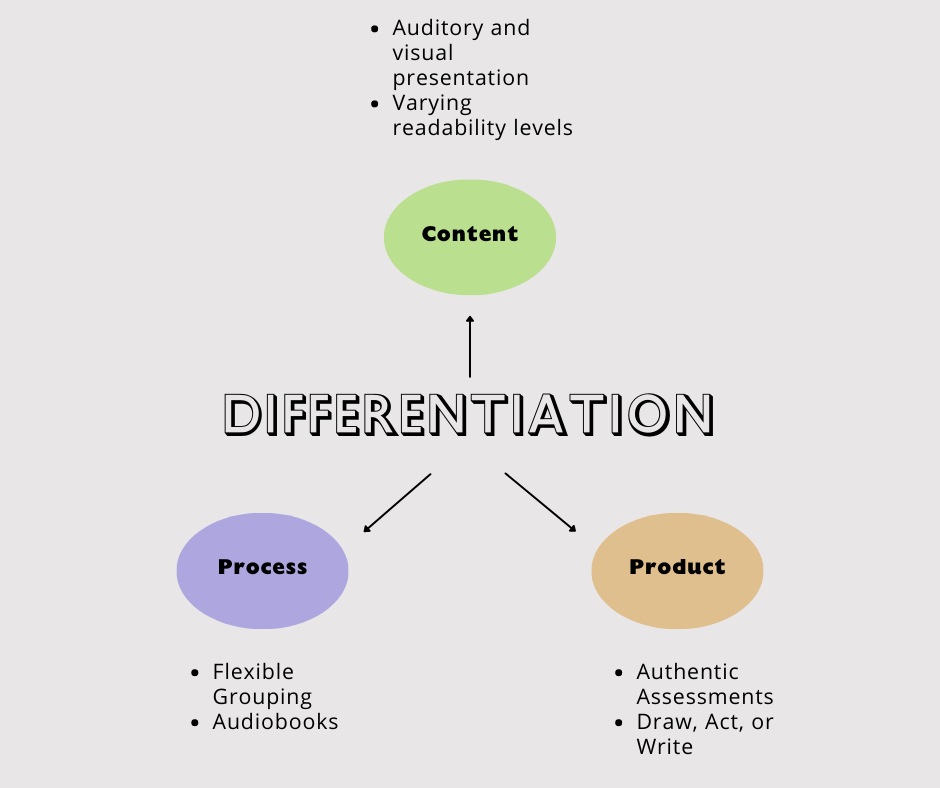
Jumpstart Differentiating Assessments and Student Products in 3 Easy
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. Review of multivariate differentiation, integration, and optimization, with applications to data science. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by.
calculus and analysis Differentiating matrix function in `Table` from
Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by.
Established Models Matrix
If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? It will always work to. Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \(.
calculus and analysis Differentiating matrix function in `Table` from
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do.
3 Ideas for Differentiating Instruction in Your Next Lesson Educator
It will always work to. Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? If.
python Error implementing differentiating matrix using numpy Stack
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. Review of multivariate differentiation, integration, and optimization, with applications to data science. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? If $m$ is your matrix, then.
Established Models Matrix
It will always work to. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \),.
calculus Differentiating the matrix square root Mathematics Stack
It will always work to. Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? If.
python Error implementing differentiating matrix using numpy Stack
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. Review of multivariate differentiation, integration, and optimization, with applications to data science. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by.
3 Ways You Can Start Differentiating Math Today Teaching with Amanda
It will always work to. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases.
It Will Always Work To.
Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors?