Differentiating Complex Functions - A complex function f(z) is continuous. In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex.
In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. A complex function f(z) is continuous. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions.
The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. A complex function f(z) is continuous.
Complex Numbers and Functions. Complex Differentiation PPT
A complex function f(z) is continuous. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. In the.
Analysis of Complex Functions and Their Properties PDF Continuous
A complex function f(z) is continuous. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable..
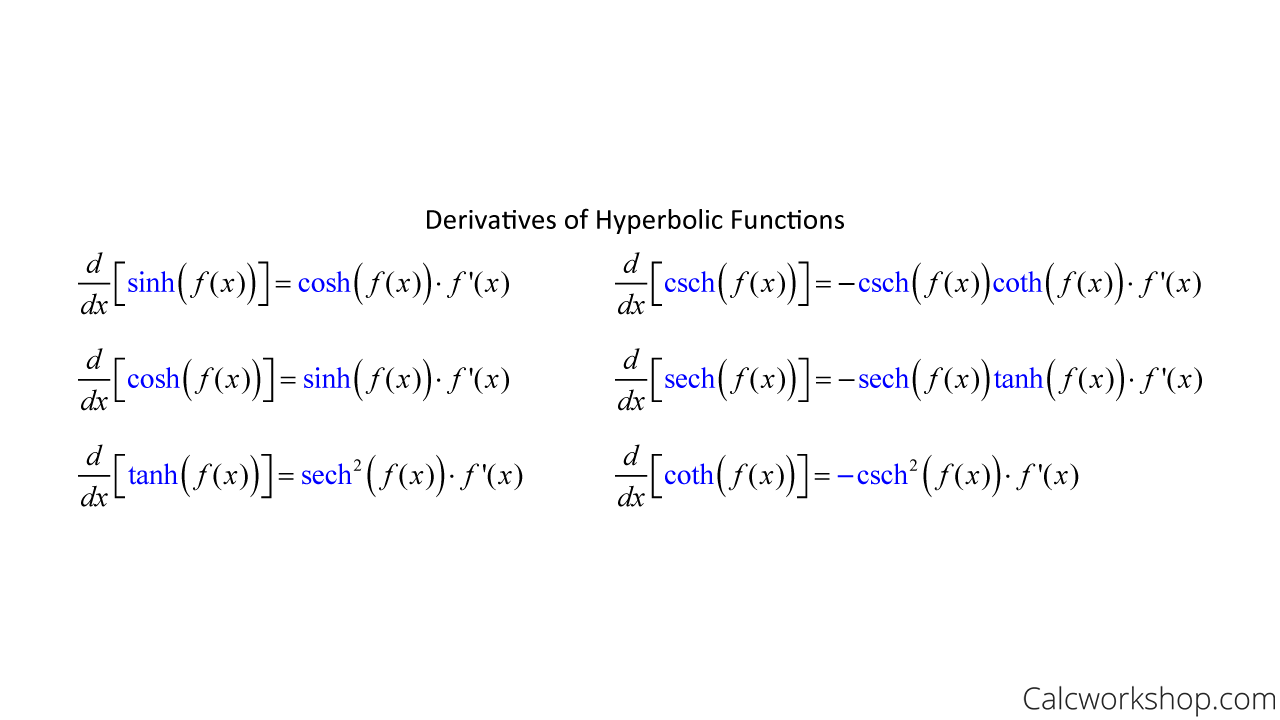
Hyperbolic Trig Functions (Explained w/ 15 Examples!)
By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions. In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. A complex function f(z) is continuous. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex..
Complex Differentiation
A complex function f(z) is continuous. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions. In the.
2Lesson 2 Differentiating Parametric Functions Solutions MATH1722
By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions. A complex function f(z) is continuous. In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex..
SOLUTION Calculus of complex functions Studypool
In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. A complex function f(z) is continuous. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions..
02b. Differentiating Exponentials and Logarithms Answers Download
In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. A complex function f(z) is continuous. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex..
Complex functions Like documents Functions of a Complex Variable
A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. A complex function f(z) is continuous. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. In the.
SOLUTION Integral of complex functions Studypool
The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. A complex function f(z) is continuous. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part..
Differentiation With Complex Functions
The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. A complex function f(z) is continuous. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions. A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. In the.
A Complex Function F(Z) Is Continuous.
A complex function \(f(z)=u(x,y)+iv(x,y)\) has a complex derivative \(f′(z)\) if and only if its real and imaginary part. In the post, we will learn about complex differentiation where we study the derivative of functions of a complex variable. The exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions—all have complex. By paying heed to this structure, we will be able to formulate a diferential calculus for complex functions.