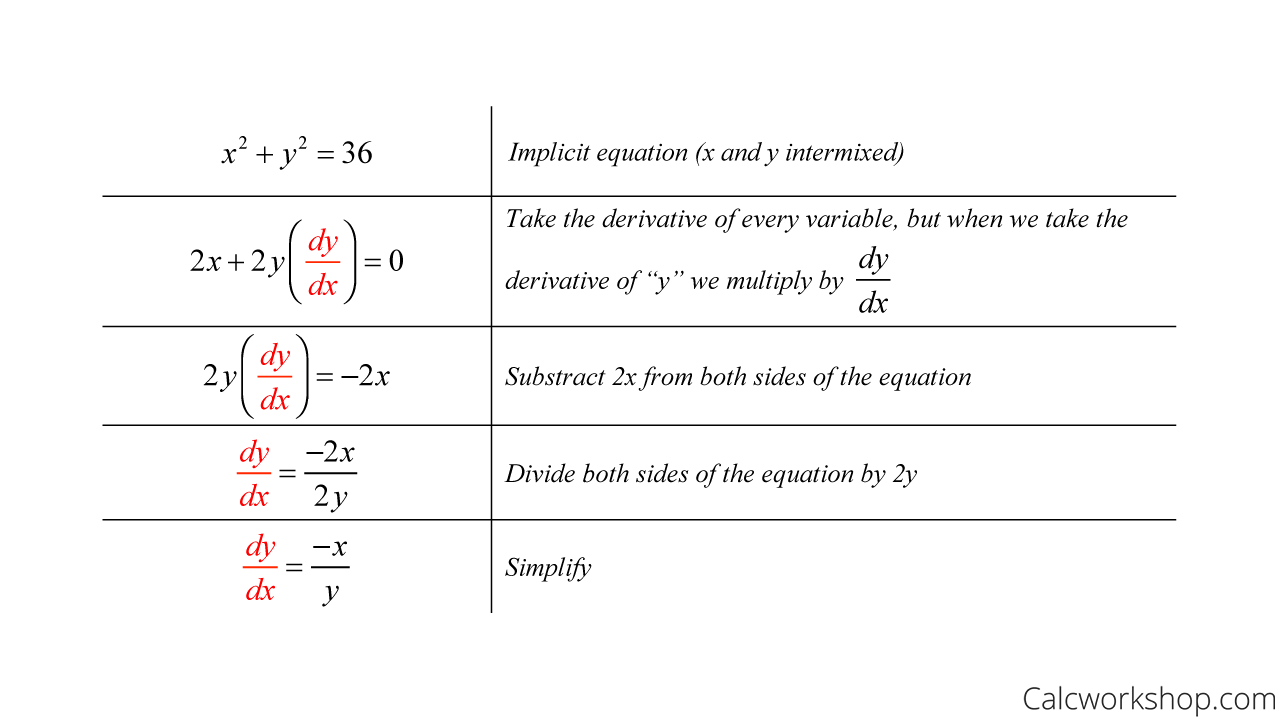Differentiation Circle - Type in any function derivative to get the solution, steps and graph. The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is difficult to calculate the. Since radii are perpendicular to tangents in a circle, the slope of the tangent line is $m$, the negative reciprocal of $m_r$. In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. If we consider the equation of a circle, $x^2+y^2=r^2$, then i understand that $dy/dx$ can be computed in the following way. When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle.
In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. Type in any function derivative to get the solution, steps and graph. Since radii are perpendicular to tangents in a circle, the slope of the tangent line is $m$, the negative reciprocal of $m_r$. If we consider the equation of a circle, $x^2+y^2=r^2$, then i understand that $dy/dx$ can be computed in the following way. When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle. The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is difficult to calculate the.
The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is difficult to calculate the. When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle. In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. Since radii are perpendicular to tangents in a circle, the slope of the tangent line is $m$, the negative reciprocal of $m_r$. If we consider the equation of a circle, $x^2+y^2=r^2$, then i understand that $dy/dx$ can be computed in the following way. Type in any function derivative to get the solution, steps and graph.
Differentiation Generic Flat icon
Since radii are perpendicular to tangents in a circle, the slope of the tangent line is $m$, the negative reciprocal of $m_r$. Type in any function derivative to get the solution, steps and graph. When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle. If we consider the.
Application of Differentiation by tutorcircle team Issuu
When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle. In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. Type in any function derivative to get the solution, steps and graph. If we consider.
Sales Differentiation Circle , Free Transparent Clipart ClipartKey
In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle. If we consider the equation of a circle, $x^2+y^2=r^2$, then i understand that $dy/dx$ can.
Differentiation Line Gradient Circle Background Icon 16831484 Vector
The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is difficult to calculate the. When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle. Type in any function derivative to get the solution,.
What is Differentiation? Learnfully
The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is difficult to calculate the. When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle. If we consider the equation of a circle, $x^2+y^2=r^2$,.
Implicit Differentiation (w/ Examples And Worksheets!)
Since radii are perpendicular to tangents in a circle, the slope of the tangent line is $m$, the negative reciprocal of $m_r$. If we consider the equation of a circle, $x^2+y^2=r^2$, then i understand that $dy/dx$ can be computed in the following way. In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which.
Differentiation Theorem Introduction, History and Solved Examples
Type in any function derivative to get the solution, steps and graph. Since radii are perpendicular to tangents in a circle, the slope of the tangent line is $m$, the negative reciprocal of $m_r$. In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. When differentiated with.
Free Differentiation Cliparts, Download Free Differentiation Cliparts
In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is difficult to calculate the. If we consider the equation of a circle,.
Differentiation icon Generic gradient outline
In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. Type in any function derivative to get the solution, steps and graph. The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is.
Differentiation Button Cartoon Vector 196836881
In summary, we discussed two methods for finding the derivative of x2 + y2 = 36, which represents a circle with radius 6. The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is difficult to calculate the. Type in any function derivative to get the.
Type In Any Function Derivative To Get The Solution, Steps And Graph.
If we consider the equation of a circle, $x^2+y^2=r^2$, then i understand that $dy/dx$ can be computed in the following way. Since radii are perpendicular to tangents in a circle, the slope of the tangent line is $m$, the negative reciprocal of $m_r$. The implicit equation x^2 + y^2 = r^2 results in a circle with a center at the origin and radius of r, but it is difficult to calculate the. When differentiated with respect to $r$, the derivative of $\pi r^2$ is $2 \pi r$, which is the circumference of a circle.