Differentiation Formulas Pdf - ( n − 1 ) ! N − 1 1 n − 1 ! ( m − n ) ! ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −. Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥
Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ( n − 1 ) ! N − 1 1 n − 1 ! ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −. ( m − n ) ! ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥
( m − n ) ! ( n − 1 ) ! ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −. ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. N − 1 1 n − 1 !
Differentiation Formulas
( n − 1 ) ! Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −. ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 ( m − n ) !
Differentiation Formulas PDF Special Functions Mathematical Objects
∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −. N − 1 1 n − 1 ! ( n − 1 ) ! ( m − n ) ! Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x.
Differentiation Formulas
Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ( m − n ) ! ( n − 1 ) ! ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −. ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥
Differentiation Formulas
∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −. Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. N − 1 1 n − 1 ! ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 ( m − n ) !
Differentiation Rules
( m − n ) ! ( n − 1 ) ! N − 1 1 n − 1 ! ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x.
SOLUTION Differentiation and integration formulas Studypool
∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 ( m − n ) ! Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −. ( n − 1 ) !
Integration And Differentiation Formula Maths 11th Notes Teachmint
N − 1 1 n − 1 ! ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 ( n − 1 ) ! Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −.
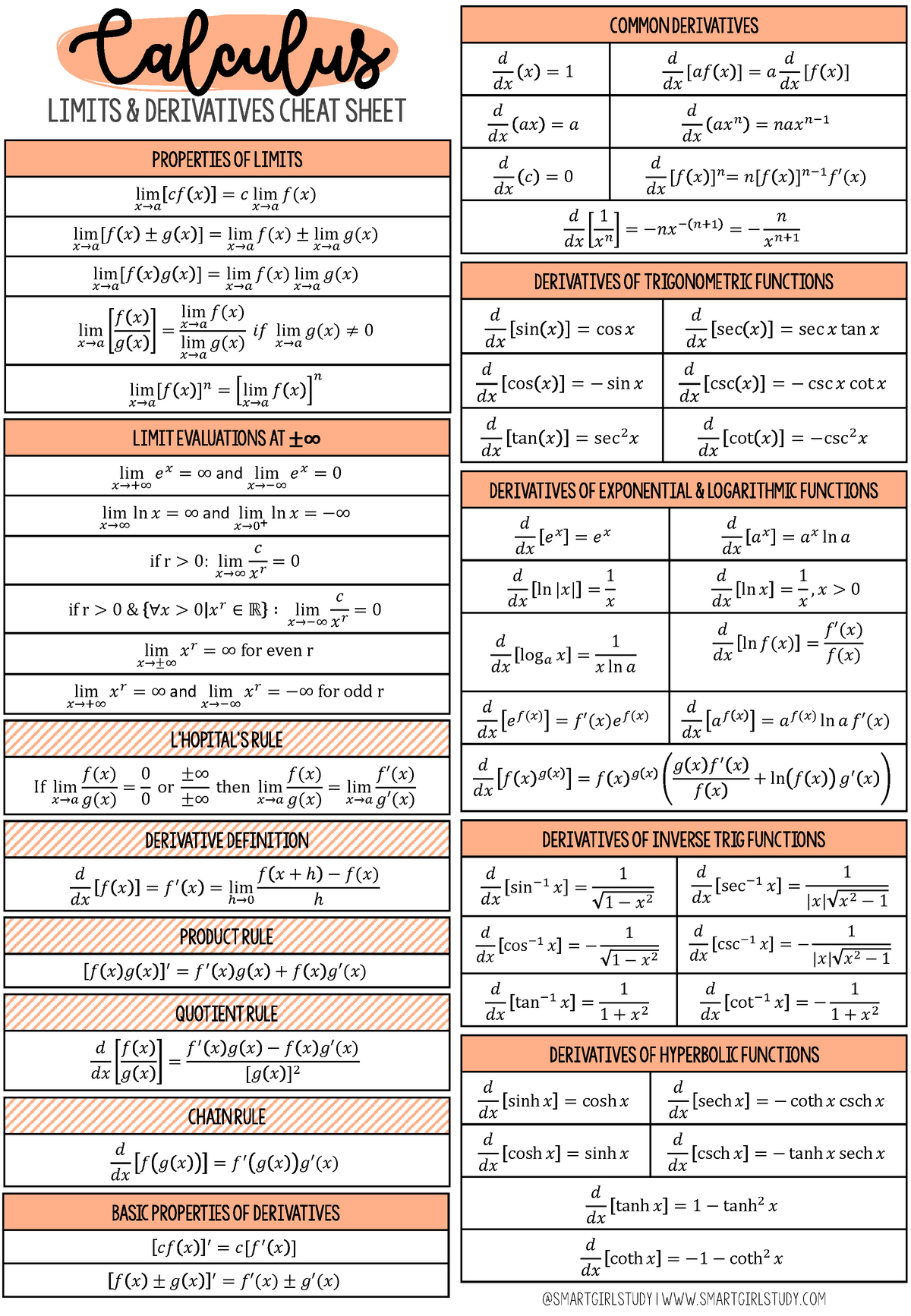
[PDF] Differentiation & Integration Formulas With Examples PDF Panot Book
( m − n ) ! ( n − 1 ) ! Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 N − 1 1 n − 1 !
Differentiation formulas for class 12 PDF Class 12 easy
∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 ( m − n ) ! N − 1 1 n − 1 ! Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −.
N − 1 1 N − 1 !
( n − 1 ) ! ∫𝑝𝑝 ′ (𝑥𝑥) cos 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥 Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x. ∫𝑝𝑝(𝑥𝑥) sin 𝑎𝑎 𝑑𝑑𝑥𝑥𝑥𝑥= −.
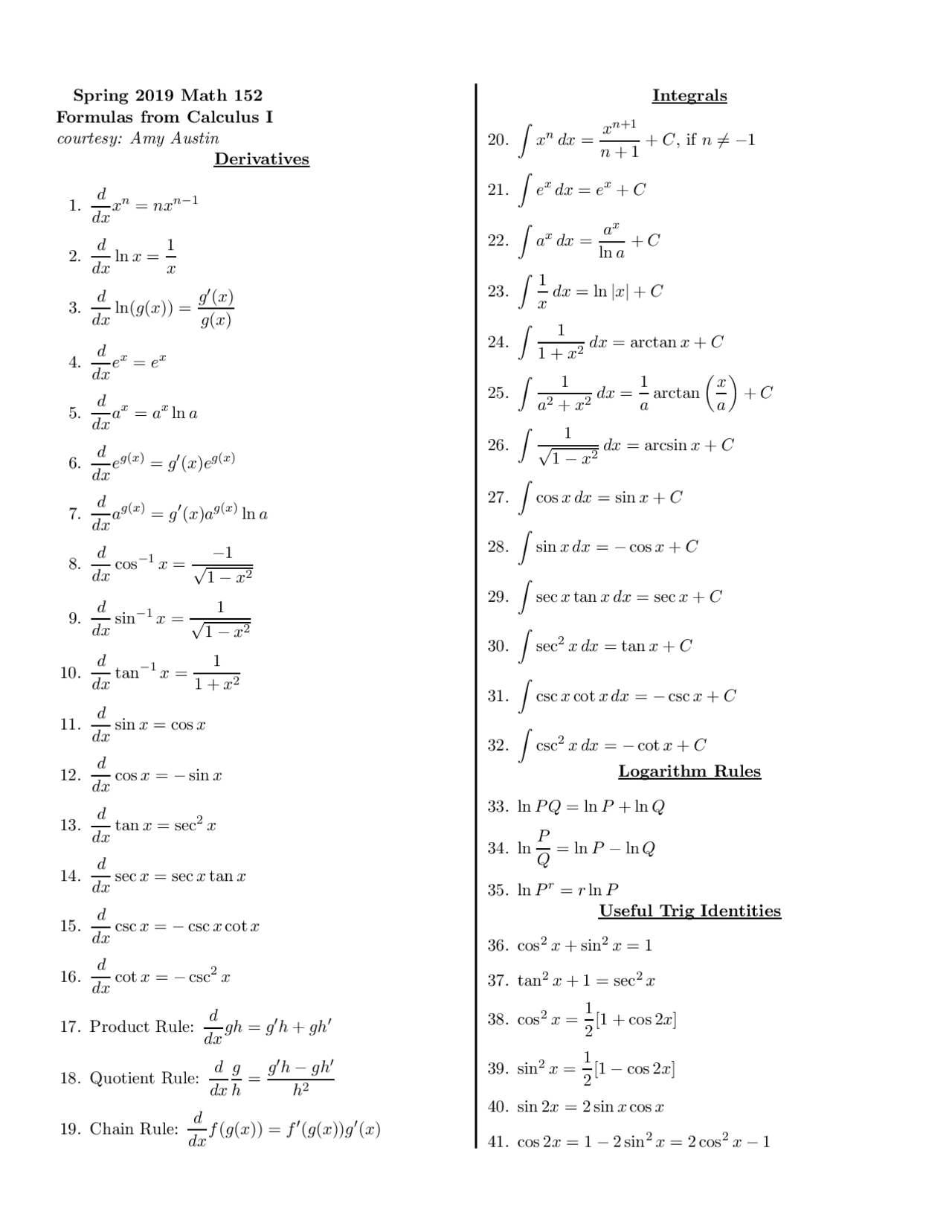





![[PDF] Differentiation & Integration Formulas With Examples PDF Panot Book](https://panotbook.com/wp-content/uploads/2022/02/Differentiation-and-Integration.jpg)

