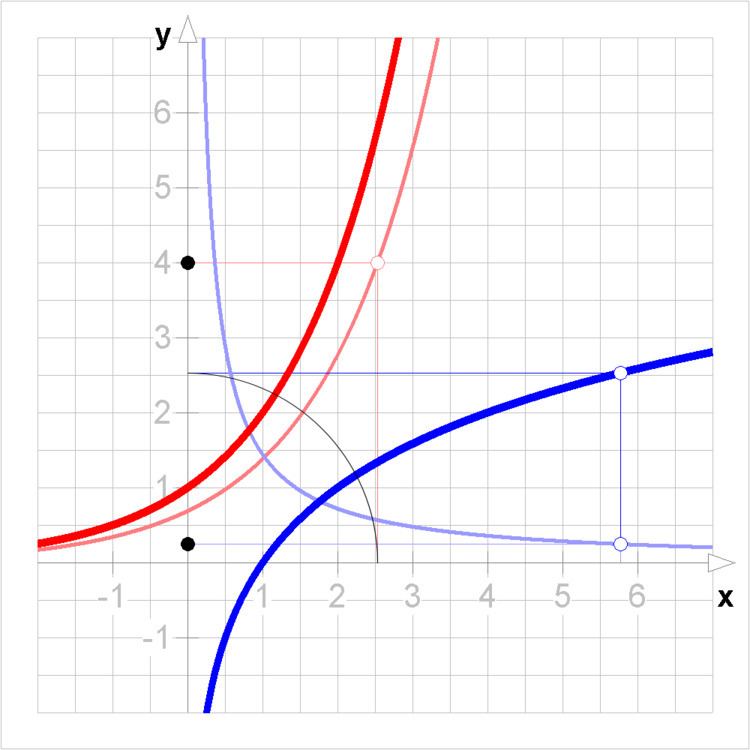
Differentiation Inverse Functions - That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b) = a f − 1 (b) = a. To do this, you only need to learn one simple formula shown below: Differentiating inverse functions is quite simple. The first good news is that even though there is no general way to compute the value of the inverse to a.
Differentiating inverse functions is quite simple. To do this, you only need to learn one simple formula shown below: The first good news is that even though there is no general way to compute the value of the inverse to a. That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b) = a f − 1 (b) = a.
That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b) = a f − 1 (b) = a. Differentiating inverse functions is quite simple. The first good news is that even though there is no general way to compute the value of the inverse to a. To do this, you only need to learn one simple formula shown below:
DIFFERENTIATION OF INVERSE TRIGONOMETRIC FUNCTIONS
The first good news is that even though there is no general way to compute the value of the inverse to a. Differentiating inverse functions is quite simple. That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b).
Inverse functions and differentiation Alchetron, the free social
The first good news is that even though there is no general way to compute the value of the inverse to a. Differentiating inverse functions is quite simple. That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b).
Inverse Functions PPT
To do this, you only need to learn one simple formula shown below: The first good news is that even though there is no general way to compute the value of the inverse to a. That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) =.
SOLUTION Differentiation inverse functions Studypool
That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b) = a f − 1 (b) = a. To do this, you only need to learn one simple formula shown below: The first good news is that even.
Using implicit differentiation for good Inverse functions.
To do this, you only need to learn one simple formula shown below: The first good news is that even though there is no general way to compute the value of the inverse to a. That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) =.
Inverse Functions Google Slides & PowerPoint
That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b) = a f − 1 (b) = a. To do this, you only need to learn one simple formula shown below: Differentiating inverse functions is quite simple. The.
SOLUTION Differentiation inverse functions Studypool
Differentiating inverse functions is quite simple. The first good news is that even though there is no general way to compute the value of the inverse to a. That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b).
Differentiation of Inverse Functions Online Calculus Course Lecturio
To do this, you only need to learn one simple formula shown below: The first good news is that even though there is no general way to compute the value of the inverse to a. Differentiating inverse functions is quite simple. That is, if f f is one to one, it has an inverse function, denoted by f−1 f −.
SOLUTION Differentiation inverse functions Studypool
That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b) = a f − 1 (b) = a. The first good news is that even though there is no general way to compute the value of the inverse.
Unit 3.3 Differentiation of General and Particular Inverse Functions
To do this, you only need to learn one simple formula shown below: That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b) = a f − 1 (b) = a. The first good news is that even.
Differentiating Inverse Functions Is Quite Simple.
To do this, you only need to learn one simple formula shown below: The first good news is that even though there is no general way to compute the value of the inverse to a. That is, if f f is one to one, it has an inverse function, denoted by f−1 f − 1, such that if f(a) = b f (a) = b, then f−1(b) = a f − 1 (b) = a.