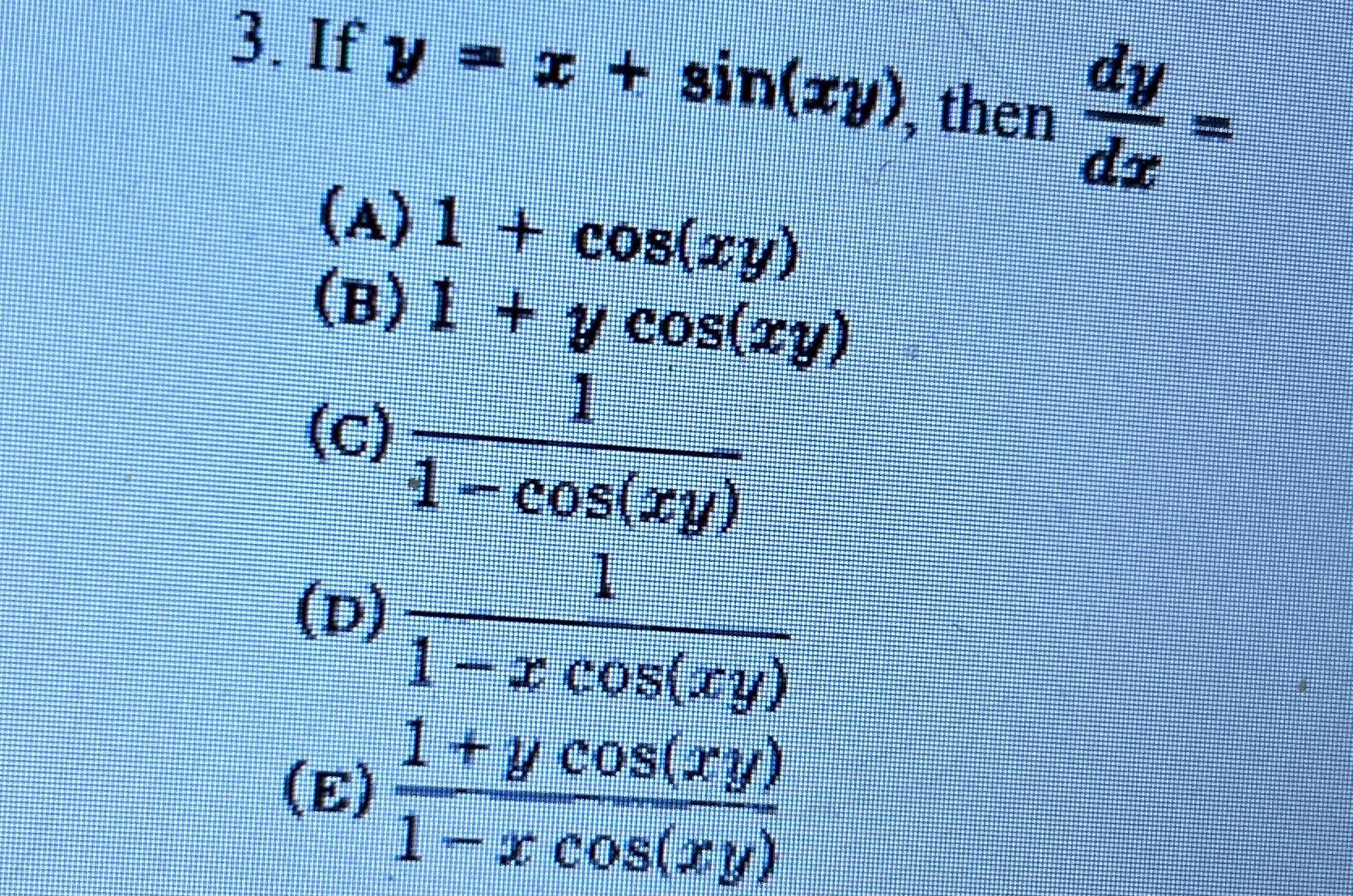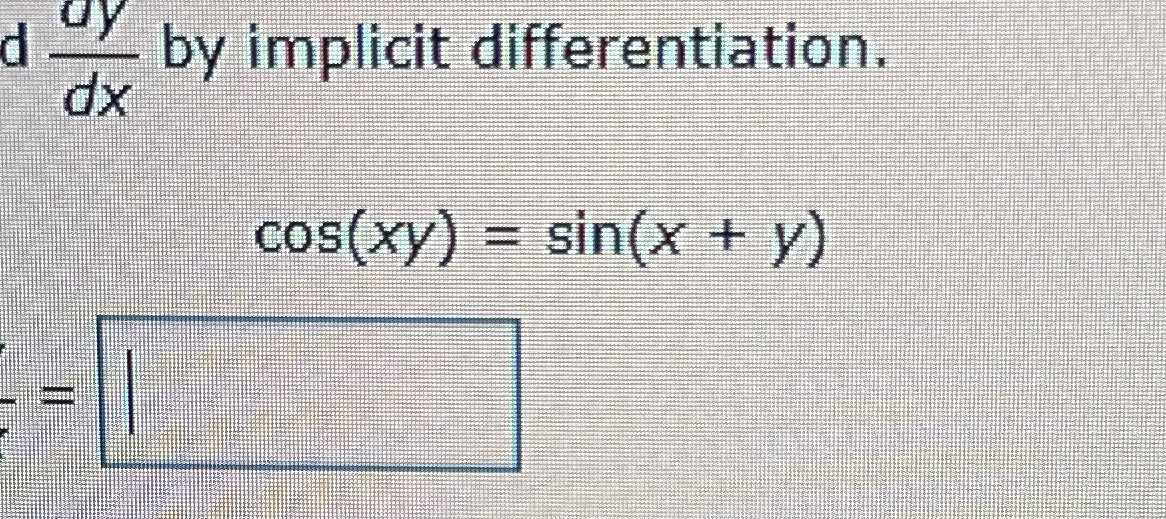Differentiation Of Cos Xy - The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. What is the derivative of cos(xy)? Replace y' y ′ with dy dx d y d x. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule:
D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: Replace y' y ′ with dy dx d y d x. What is the derivative of cos(xy)? The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x).
Replace y' y ′ with dy dx d y d x. The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. What is the derivative of cos(xy)? D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule:
Solved Use implicit differentiation to find dy/dx. Cos xy +
Replace y' y ′ with dy dx d y d x. D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more What is the derivative of cos(xy)? D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the.
Solved If y=x+sin(xy), then
D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more Replace y' y ′ with dy dx d y d x.
Solved ddydx by implicit differentiation.cos(xy)=sin(x+y)
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: The differentiation of trigonometric functions is the mathematical process.
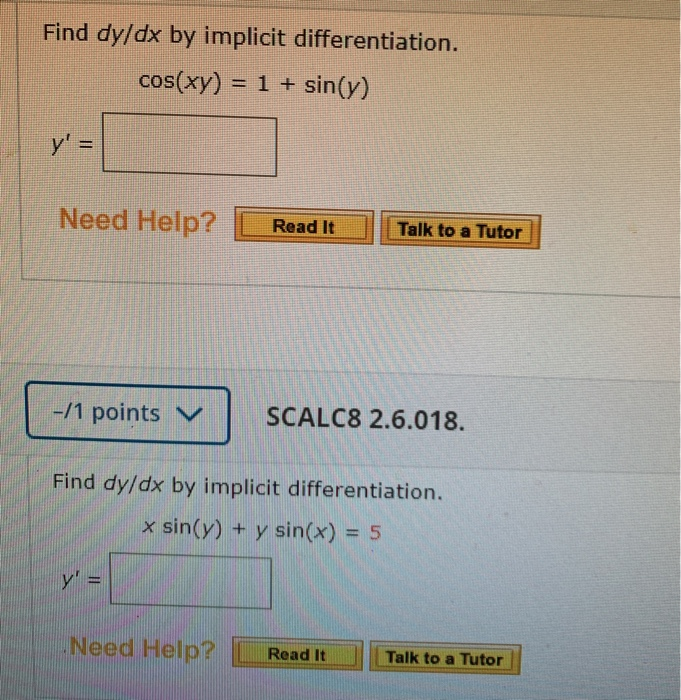
[Solved] Find dy / dx by implicit differentiation. cos( xy ) = 1 + sin
\int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more Replace y' y ′ with dy dx d y d x. What is the derivative of cos(xy)? The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. Differentiate using the chain rule, which states that d dx [f (g(x))] d d.
Solved Given the following differential equation (cos(xy) +
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). What is the derivative of cos(xy)? D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. Replace y' y ′ with.
[Solved] Find dy / dx by implicit differentiation. cos( xy ) = 1 + sin
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). Replace y' y ′ with dy dx d y d.
Solved Find dy/dx by implicit differentiation. cos(xy) = 1 +
Replace y' y ′ with dy dx d y d x. What is the derivative of cos(xy)? Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n}.
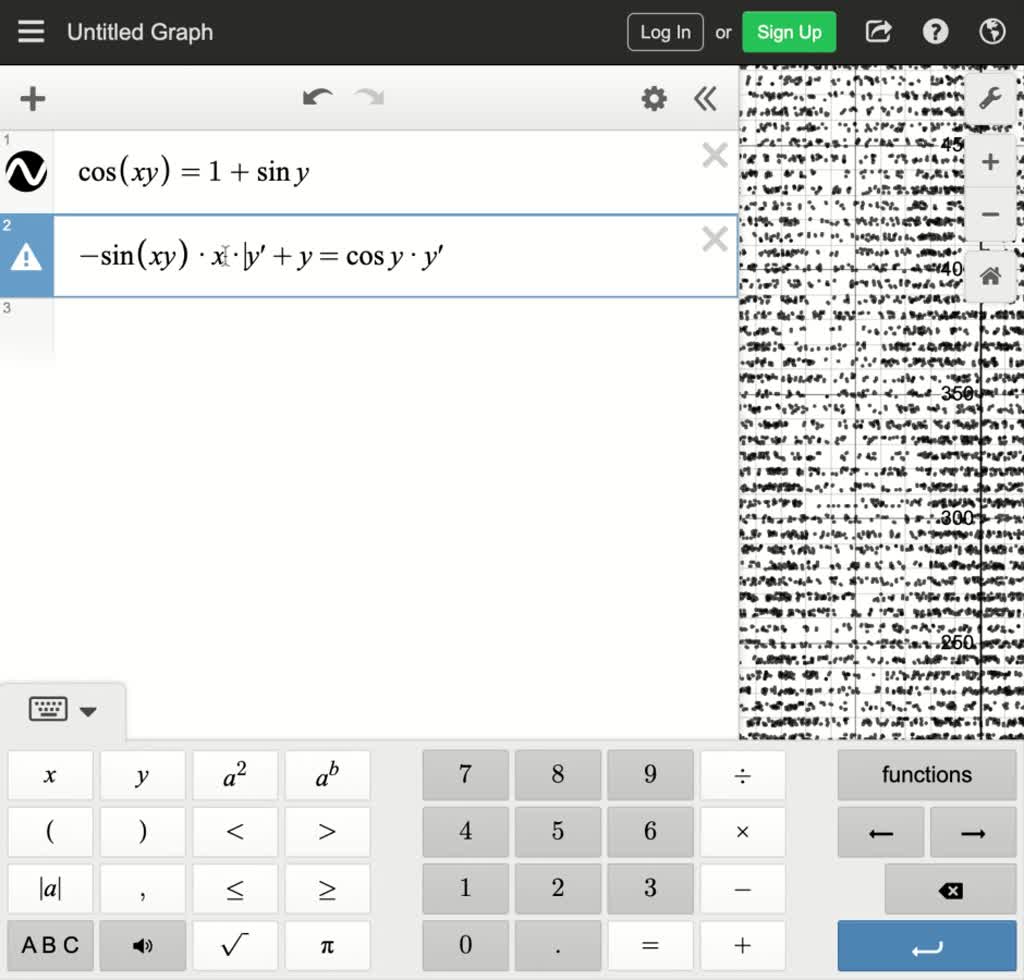
SOLVED Find dy/dx by implicit differentiation. cos(xy) = 1 + siny
D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. Replace y' y ′ with dy dx d y d x.
Solved Given the following differential equation ( cos(xy?)
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then.
Solved Find dy/dx by implicit differentiation. cos (xy)=sin (x+y) dy
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more What is the derivative of cos(xy)? Free math problem solver answers your algebra, geometry, trigonometry,.
Free Math Problem Solver Answers Your Algebra, Geometry, Trigonometry, Calculus, And Statistics.
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. Replace y' y ′ with dy dx d y d x. D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule:
\Int E^x\Cos (X)Dx \Int_{0}^{\Pi}\Sin(X)Dx \Sum_{N=0}^{\Infty}\Frac{3}{2^N} Show More
What is the derivative of cos(xy)? The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change.