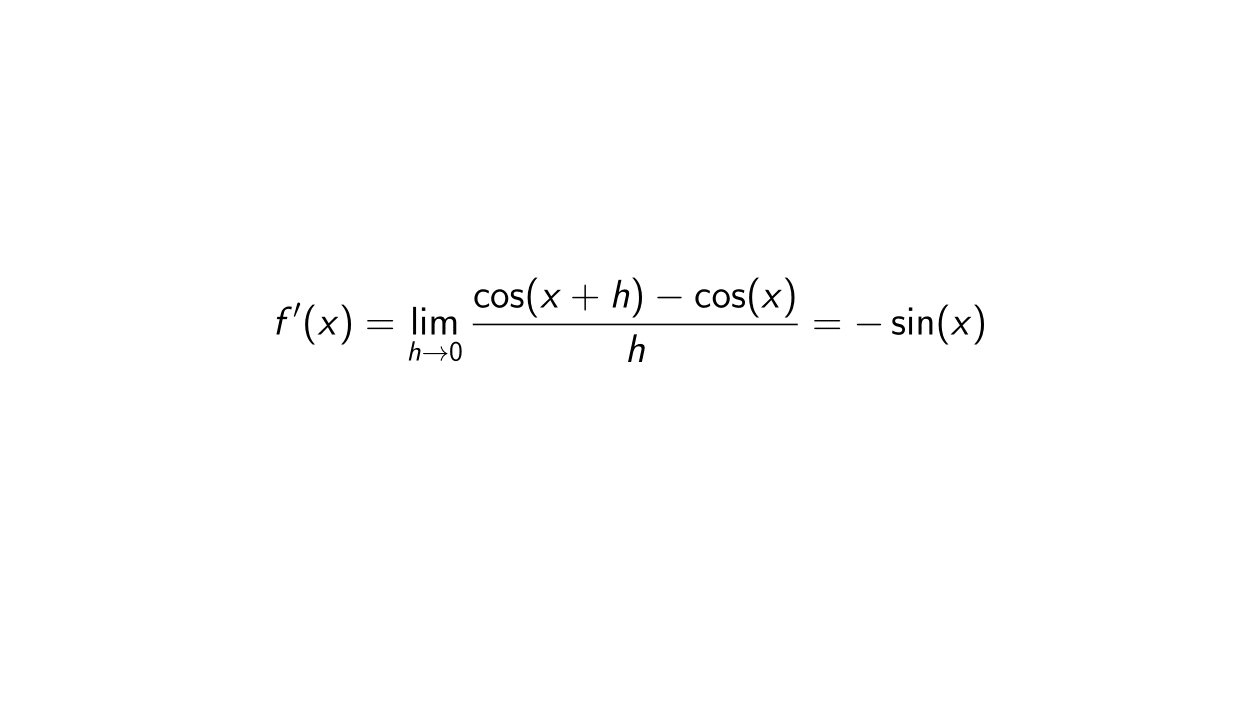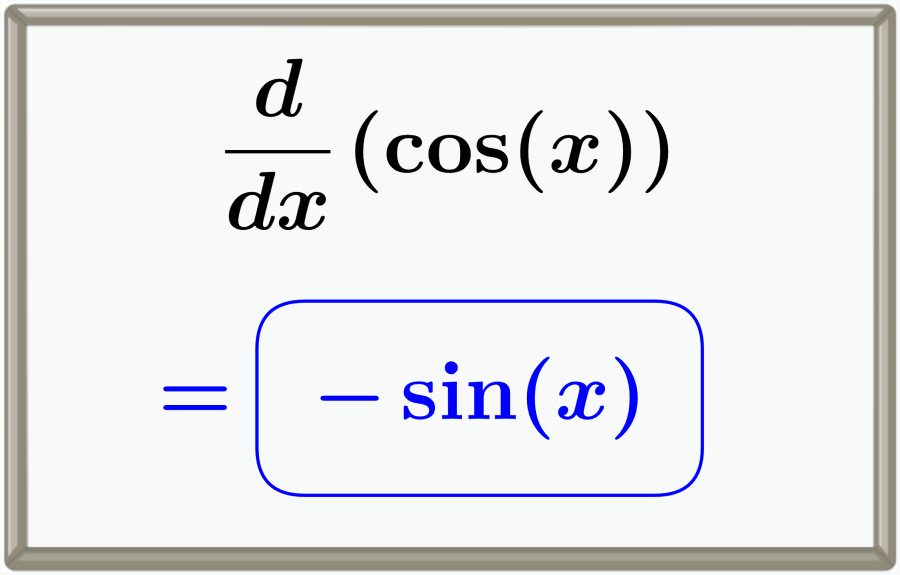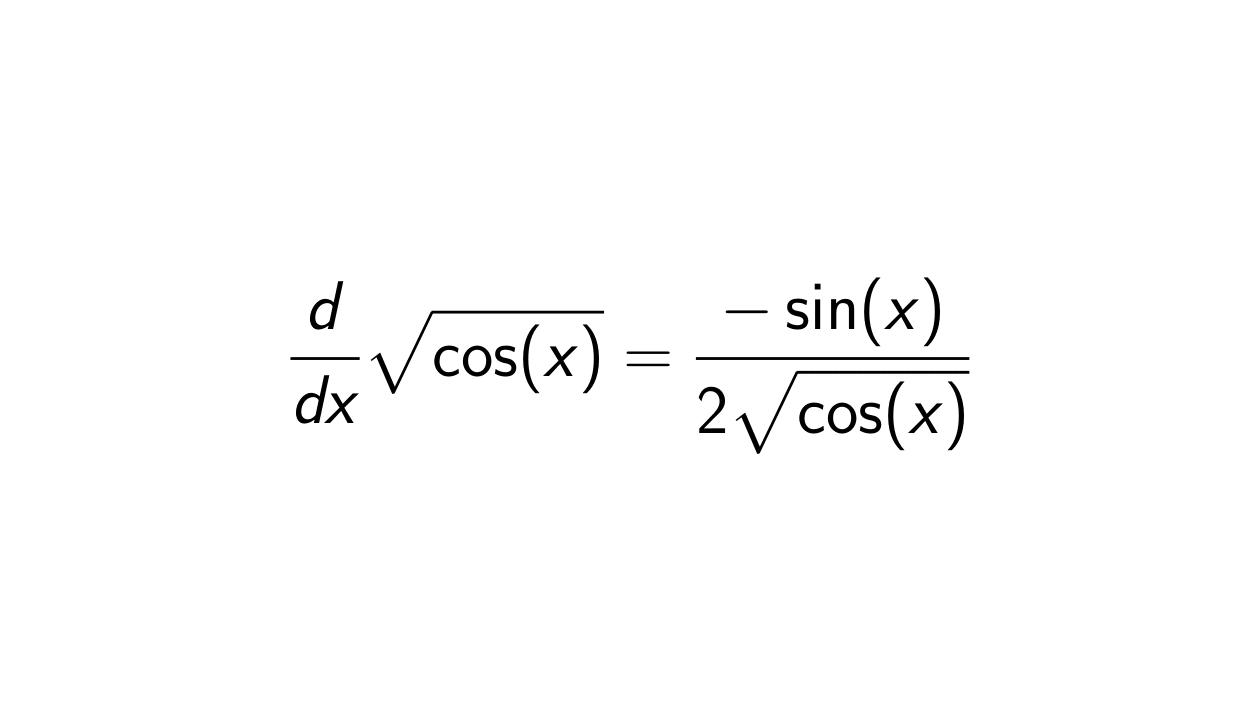Differentiation Of Cosx - In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. We use a technique called logarithmic differentiation to differentiate this kind of function. Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : The 2 which will be useful here are: Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then
We use a technique called logarithmic differentiation to differentiate this kind of function. Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. The 2 which will be useful here are: Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions :
We use a technique called logarithmic differentiation to differentiate this kind of function. Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : The 2 which will be useful here are:
to how cos(x) solve 1 5576666 cosx/1 sinx cosx=tan(x/2)
Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : The 2 which will be useful here are: We use a technique called logarithmic differentiation to differentiate this kind of function. In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. Reminder ∙ d dx (sinx) = cosx and d dx (cosx).
Ex 5.7, 3 Find second order derivatives of x cosx Ex 5.7
In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then We use a technique called logarithmic differentiation to differentiate this kind of function. The 2.
Differentiation of Trigonometric Functions Kunduz
The 2 which will be useful here are: Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x).
Derivative of Cosine, cos(x) Formula, Proof, and Graphs Neurochispas
The 2 which will be useful here are: In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : We use a technique called logarithmic differentiation to differentiate this kind of function. Reminder ∙ d dx (sinx) = cosx and d dx (cosx).
y = cot^1(cosxsinx/cosx+sinx) Find the derivative Maths Inverse
Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. The 2 which will be useful here are: We use a technique called logarithmic differentiation.
Derivative of Cos(x) Formula, Proof in Easy Steps, Formula, Solved
Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then The 2 which will be useful here are: We use a technique called logarithmic differentiation to differentiate this kind of function. Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : In short,.
Differentiating f(x)=cosx Using a Specific Rule Calculus
The 2 which will be useful here are: In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then We use a technique called logarithmic differentiation.
Ex 5.7, 3 Find second order derivatives of x cosx Ex 5.7
In short, we let y = (cos (x))^x, then, ln (y) = ln ( (cos (x))^x) ln (y. Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then We use a technique called logarithmic differentiation to differentiate this kind of function. Dy/dx=sinx*sin (cosx).
What is the differentiation of cosx with respect to x equals to?
Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then The 2 which will be useful here are: We use a technique called logarithmic differentiation to differentiate this kind of function. Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : In short,.
Derivative of square root cos(x) Detailed Solution Epsilonify
Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : We use a technique called logarithmic differentiation to differentiate this kind of function. In short, we let y = (cos (x))^x, then, ln.
In Short, We Let Y = (Cos (X))^X, Then, Ln (Y) = Ln ( (Cos (X))^X) Ln (Y.
Dy/dx=sinx*sin (cosx) first from the differentiation of trigonometric functions : The 2 which will be useful here are: We use a technique called logarithmic differentiation to differentiate this kind of function. Reminder ∙ d dx (sinx) = cosx and d dx (cosx) = − sinx to differentiate xsinx use the product rule given f (x) = g(x)h(x) then