Differentiation Of Force - For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In a scenario where you consider a. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. Why is the force being the differential of a potential equivalent to it being a conservative force? Force is the time derivative of momentum: In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by.
In a scenario where you consider a. Why is the force being the differential of a potential equivalent to it being a conservative force? For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. Force is the time derivative of momentum: In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t.
For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In a scenario where you consider a. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. Why is the force being the differential of a potential equivalent to it being a conservative force? Force is the time derivative of momentum:
Differentiation From First Principles Gradient Of A Curve
In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. In a scenario where you consider a. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. Why is the force being the.
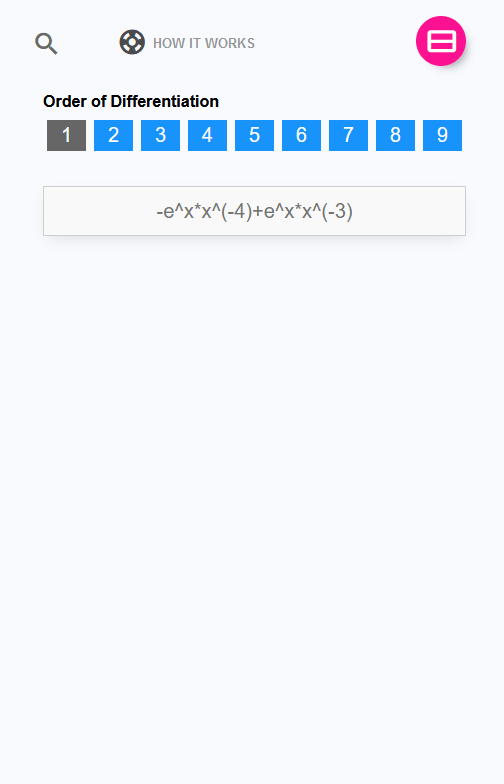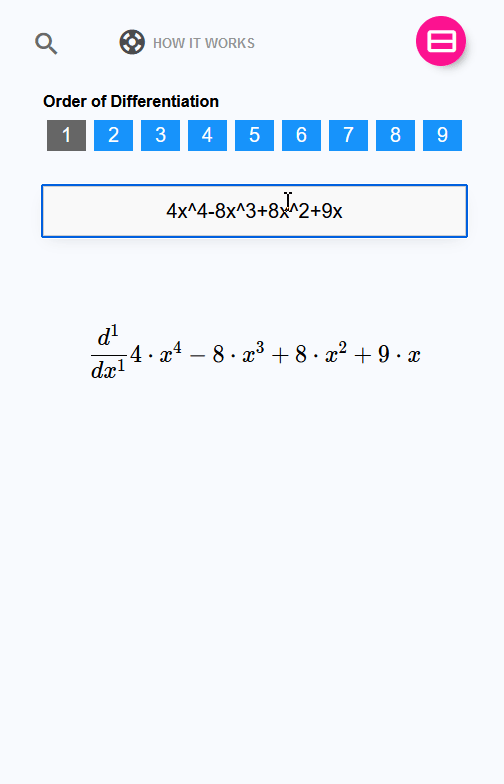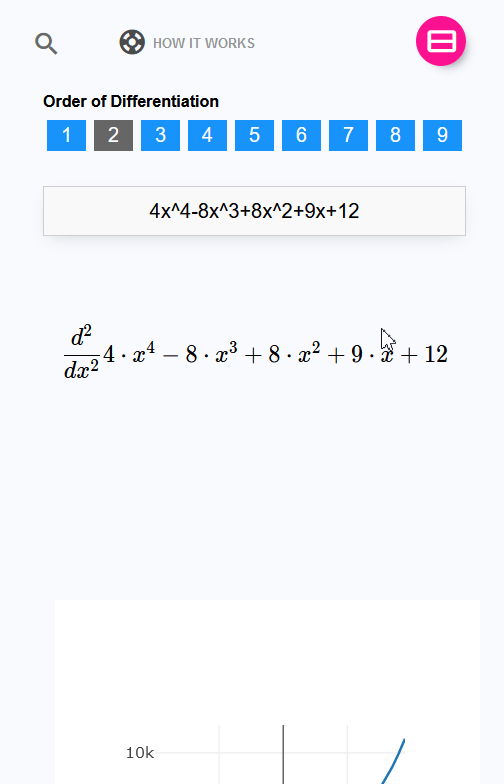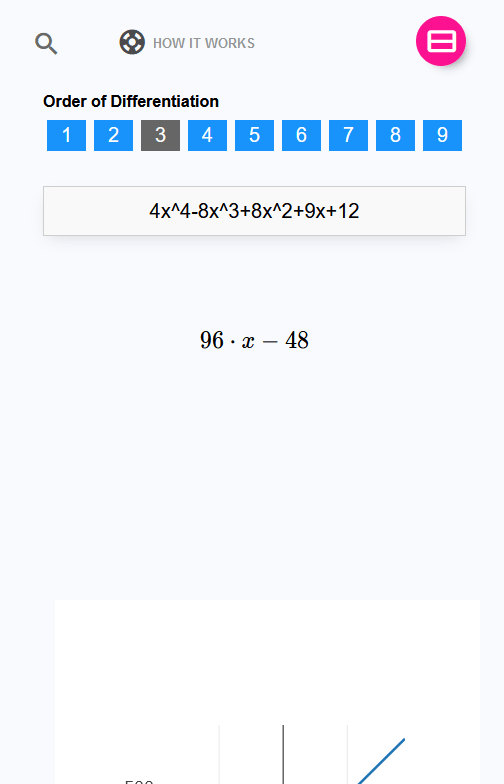
force = mass × acceleration =2.5×12=30 N WH. BASED ON DIFFERENTIATION 1.
Force is the time derivative of momentum: In a scenario where you consider a. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In my lecture today my.
Differentiation An Important Marketing Strategy Technique Career Parts
In a scenario where you consider a. Force is the time derivative of momentum: For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. Why is.
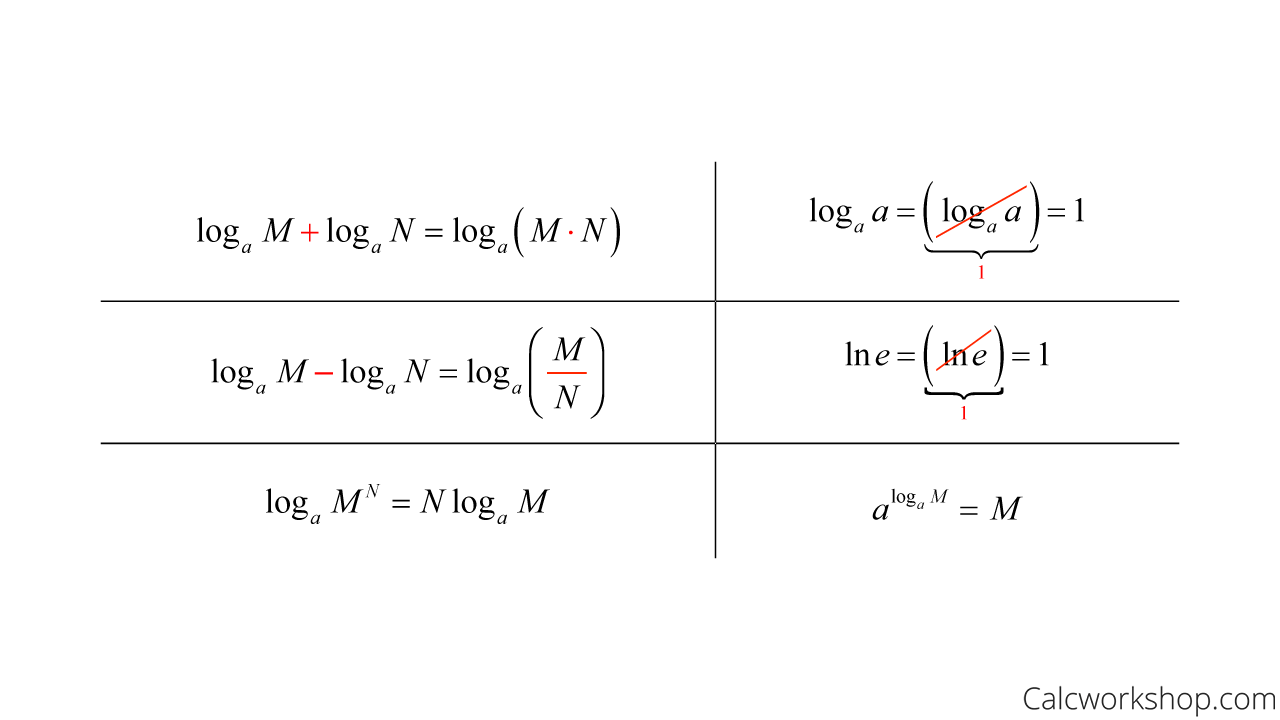
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
In a scenario where you consider a. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. Force is the time derivative of momentum: For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In my lecture today my.
Master Template
In a scenario where you consider a. Force is the time derivative of momentum: For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. Why is the force being the differential of a potential equivalent to it being a conservative force? F = dp dt ⇔ dp =f dt f =.
Differentiation Formulas Toppers Bulletin
For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. Why is the force being the differential of a potential equivalent to it being a conservative force? Force is the time derivative of momentum: In my lecture today my professor briefly mentioned that force is the derivative of energy but i.
Differentiation Button Cartoon Vector 196836881
For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. Force is the time derivative of momentum: Why is the force being the differential of a.
Product Differentiation How to Strategize for Business Success ClickUp
Force is the time derivative of momentum: In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. In a scenario where you consider.
Differentiation doesn’t matter, distinctiveness does
F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In a scenario where you consider a. Force is the time derivative of momentum: Why is the force being.
Product Differentiation Examples And Strategies Glossary, 58 OFF
Why is the force being the differential of a potential equivalent to it being a conservative force? For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. In a.
F = Dp Dt ⇔ Dp =F Dt F = D P → D T ⇔ D P = F D T.
In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. Force is the time derivative of momentum: For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. Why is the force being the differential of a potential equivalent to it being a conservative force?