Differentiation Of Sin Xy - Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). Differentiate the right side of the equation. The left side would simply give you #dy/dx#. You simply differentiate both sides with respect to #x#. For the right side, however,. The derivative of y y with respect to x x is y' y ′. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. Differentiate both sides of the equation. What is the derivative of the function y = sin(xy)? Type in any function derivative to get the solution, steps and graph.
What is the derivative of the function y = sin(xy)? Type in any function derivative to get the solution, steps and graph. The derivative of y y with respect to x x is y' y ′. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). For the right side, however,. Differentiate both sides of the equation. You simply differentiate both sides with respect to #x#. The left side would simply give you #dy/dx#. Differentiate the right side of the equation. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,.
What is the derivative of the function y = sin(xy)? Differentiate the right side of the equation. You simply differentiate both sides with respect to #x#. Differentiate both sides of the equation. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). Type in any function derivative to get the solution, steps and graph. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. For the right side, however,. The left side would simply give you #dy/dx#. The derivative of y y with respect to x x is y' y ′.
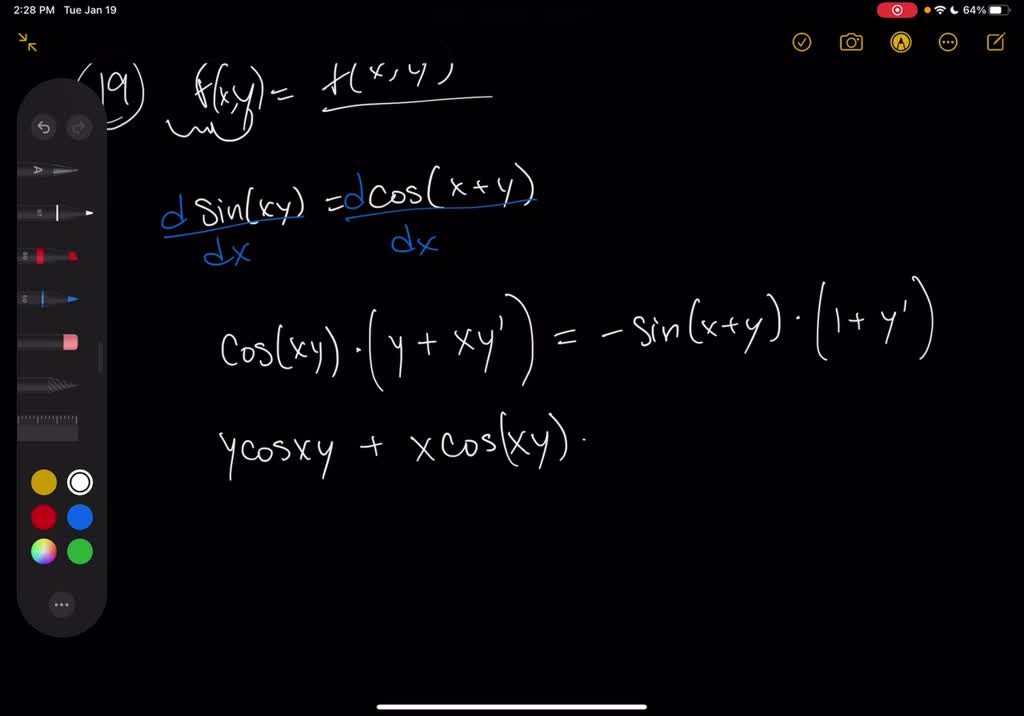
Solved Implicit differentiation sin (x + y)^2 = (xy)^3 8
For the right side, however,. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). You simply differentiate both sides with respect to #x#. What is the derivative of the function y.
[Solved] . sin xy = x 2 + y. y Cos xy = X lue in the red box is lue
You simply differentiate both sides with respect to #x#. Differentiate both sides of the equation. The derivative of y y with respect to x x is y' y ′. Differentiate the right side of the equation. The left side would simply give you #dy/dx#.
Solved Find dy/dx by implicit differentiation. cos (xy)=sin (x+y) dy
Type in any function derivative to get the solution, steps and graph. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. The derivative of y y with respect to x x is y' y ′. Differentiate the right side of the equation. For the right side, however,.
Solved Use implicit differentiation to find dy/dx. Cos xy +
Differentiate the right side of the equation. For the right side, however,. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. Differentiate both sides of the equation. What is the derivative of the function y = sin(xy)?
Find dy/dx by implicit differentiation. sin(xy) = cos(x+y) Numerade
Differentiate both sides of the equation. The left side would simply give you #dy/dx#. For the right side, however,. Type in any function derivative to get the solution, steps and graph. You simply differentiate both sides with respect to #x#.
[Solved] Find dy / dx by implicit differentiation. cos( xy ) = 1 + sin
The derivative of y y with respect to x x is y' y ′. Type in any function derivative to get the solution, steps and graph. Differentiate both sides of the equation. The left side would simply give you #dy/dx#. Differentiate the right side of the equation.
Solved If y=x+sin(xy), then
What is the derivative of the function y = sin(xy)? You simply differentiate both sides with respect to #x#. For the right side, however,. Differentiate both sides of the equation. The derivative of y y with respect to x x is y' y ′.
Solved For Sin (XY) X = 0 Using Implicit Differentiatio...
Type in any function derivative to get the solution, steps and graph. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. For the right side, however,. The left side would simply give you #dy/dx#. Differentiate both sides of the equation.
Solved 1. Determine The Derivative Of X Sin^1x/ Square R...
The left side would simply give you #dy/dx#. The derivative of y y with respect to x x is y' y ′. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. For the right side, however,. What is the derivative of the function y = sin(xy)?
How do you differentiate y=sin(xy)? Socratic
Differentiate the right side of the equation. For the right side, however,. Type in any function derivative to get the solution, steps and graph. The derivative of y y with respect to x x is y' y ′. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,.
The Derivative Of Y Y With Respect To X X Is Y' Y ′.
What is the derivative of the function y = sin(xy)? Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. Type in any function derivative to get the solution, steps and graph. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x).
Differentiate Both Sides Of The Equation.
Differentiate the right side of the equation. For the right side, however,. The left side would simply give you #dy/dx#. You simply differentiate both sides with respect to #x#.
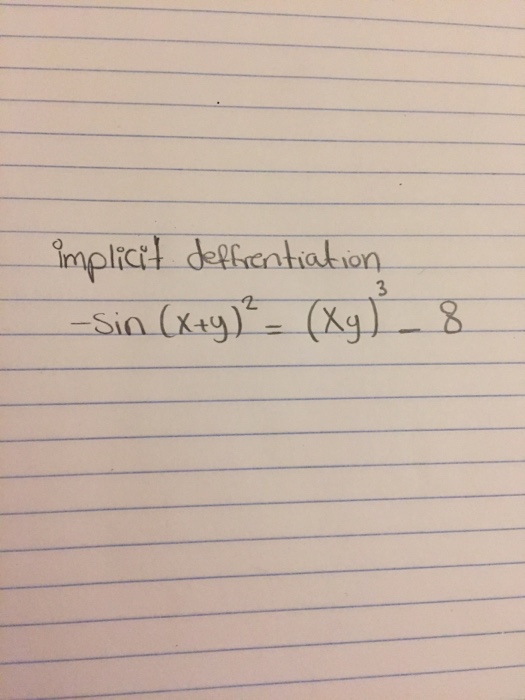

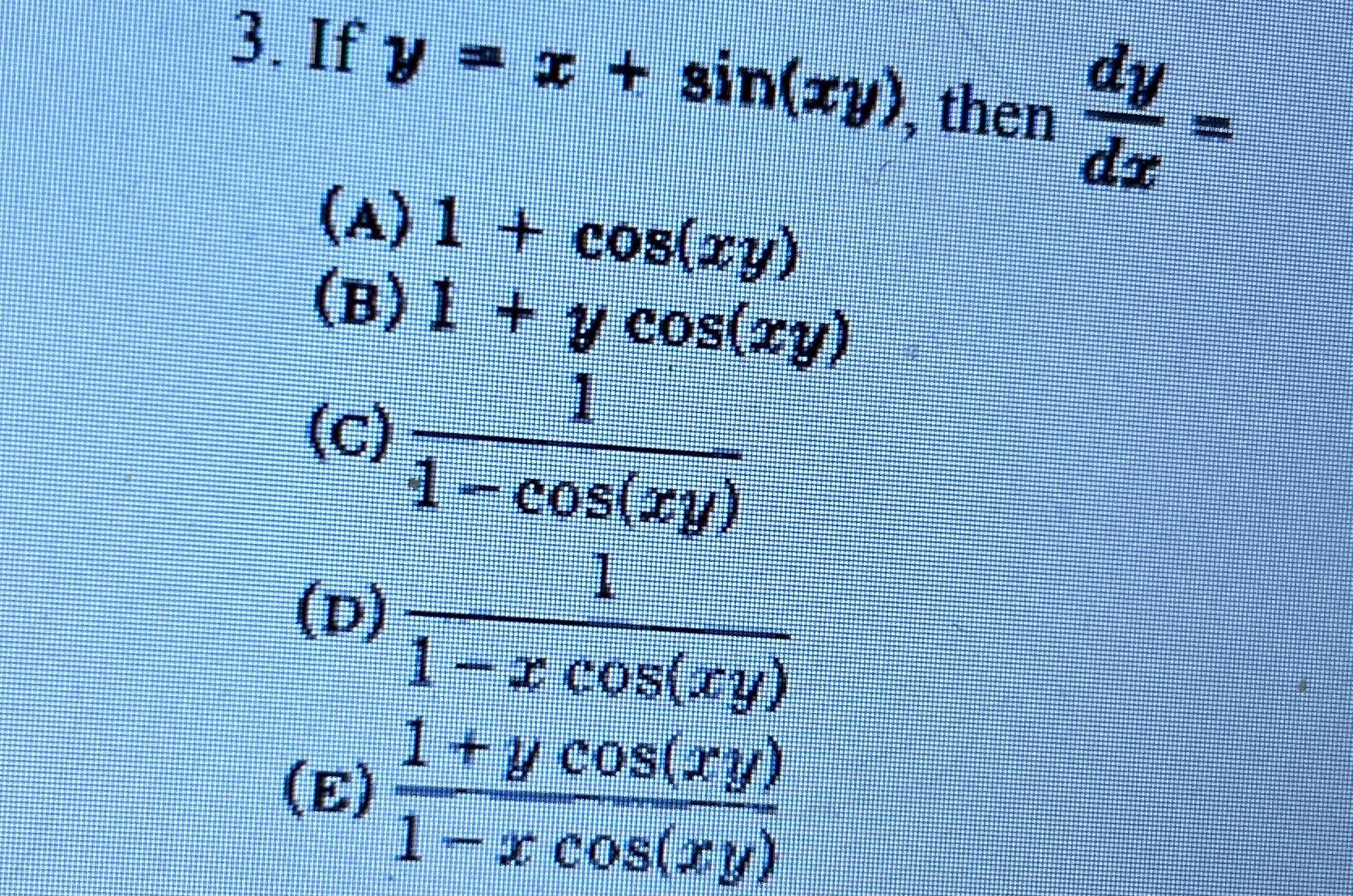


.png)