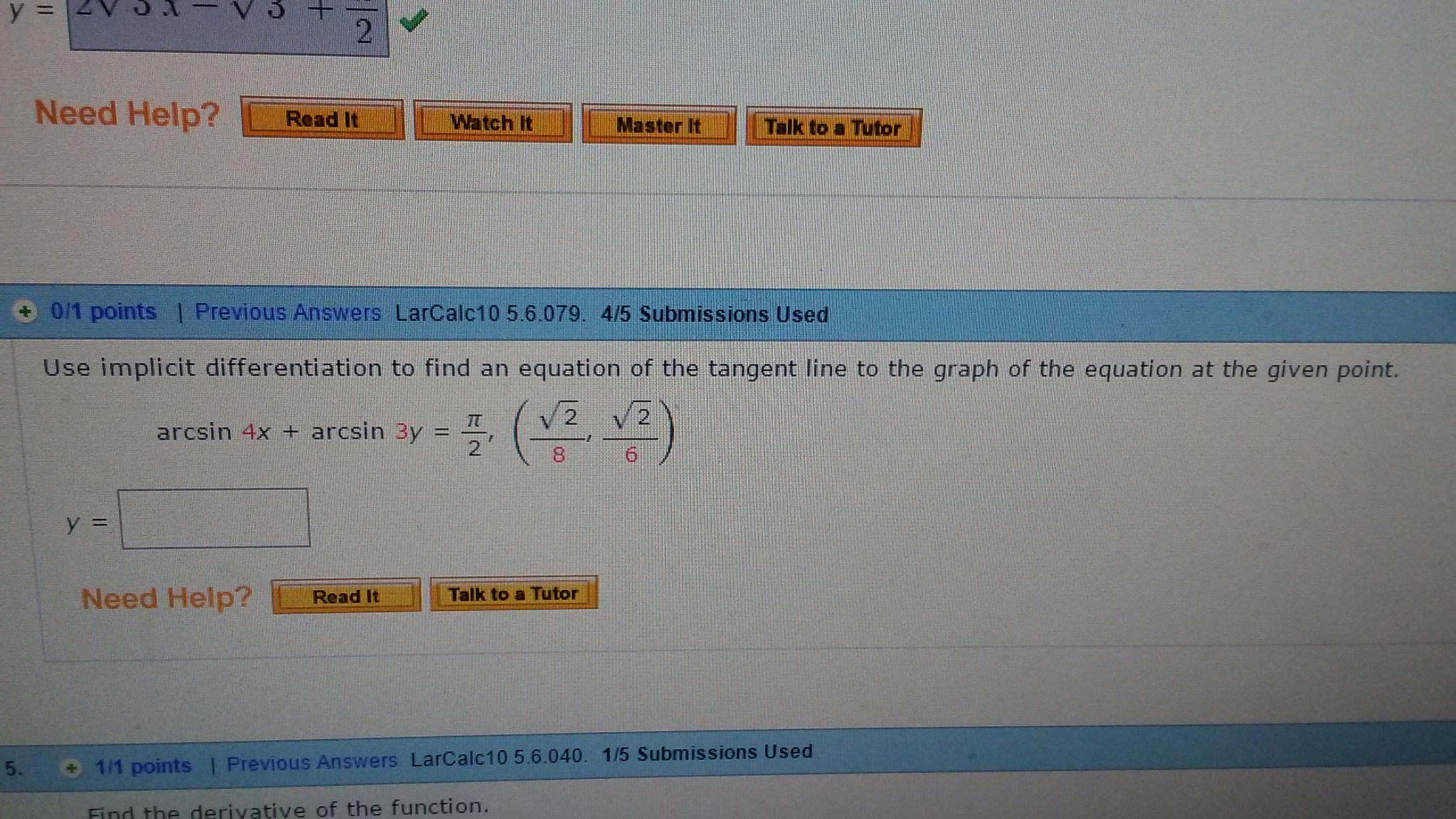
Equation Of Tangent Line Implicit Differentiation - Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). First differentiate implicitly, then plug in. To find the equation of the tangent line using implicit differentiation, follow three steps. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations).
Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). To find the equation of the tangent line using implicit differentiation, follow three steps. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). First differentiate implicitly, then plug in.
To find the equation of the tangent line using implicit differentiation, follow three steps. Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). First differentiate implicitly, then plug in. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations).
Equation of the tangent line using implicit differentiation — Krista
First differentiate implicitly, then plug in. To find the equation of the tangent line using implicit differentiation, follow three steps. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\).
Solved Use implicit differentiation to find an equation of
Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). To find the equation of the tangent line using implicit differentiation, follow three steps. First differentiate implicitly, then plug in.
Answered Use implicit differentiation to find an… bartleby
We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). First differentiate implicitly, then plug in. To find the equation of the tangent line using implicit differentiation, follow three steps. Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\).
Answered Use implicit differentiation to find an… bartleby
First differentiate implicitly, then plug in. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). To find the equation of the tangent line using implicit differentiation, follow three steps. Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\).
Solved Use implicit differentiation to find an equation of
First differentiate implicitly, then plug in. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). To find the equation of the tangent line using implicit differentiation, follow three steps. Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\).
Answered Use implicit differentiation to find an… bartleby
Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). To find the equation of the tangent line using implicit differentiation, follow three steps. First differentiate implicitly, then plug in.
Equation of the tangent line using implicit differentiation — Krista
Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). To find the equation of the tangent line using implicit differentiation, follow three steps. First differentiate implicitly, then plug in.
Higher Derivatives Implicit Differentiation Equation of Tangent and
We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). To find the equation of the tangent line using implicit differentiation, follow three steps. First differentiate implicitly, then plug in.
Solved Use Implicit Differentiation To Find An Equation O...
To find the equation of the tangent line using implicit differentiation, follow three steps. Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). First differentiate implicitly, then plug in. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations).
Solved Use implicit differentiation to find an equation of
We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). First differentiate implicitly, then plug in. To find the equation of the tangent line using implicit differentiation, follow three steps.
We Use Implicit Differentiation To Find Derivatives Of Implicitly Defined Functions (Functions Defined By Equations).
To find the equation of the tangent line using implicit differentiation, follow three steps. Example 4 find the equation of the tangent line to \[{x^2} + {y^2} = 9\] at the point \(\left( {2,\,\,\sqrt 5 } \right)\). First differentiate implicitly, then plug in.