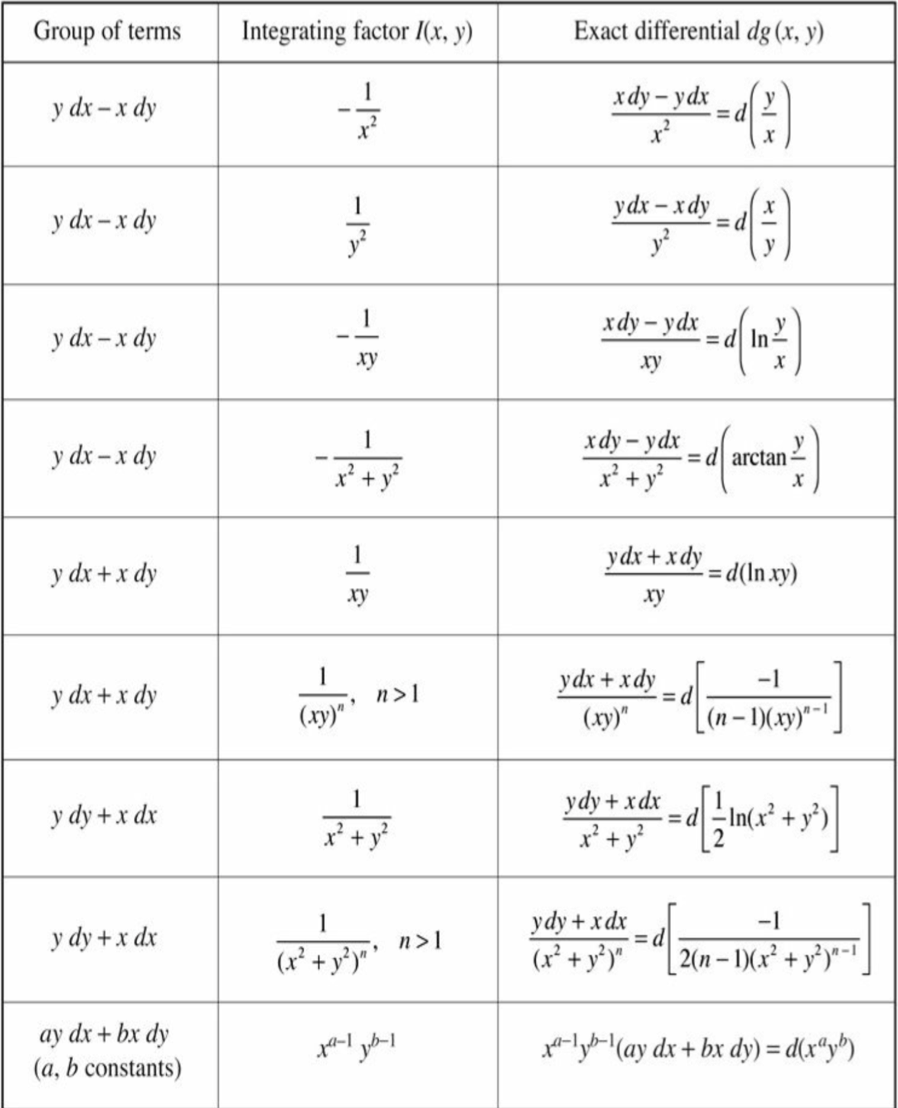
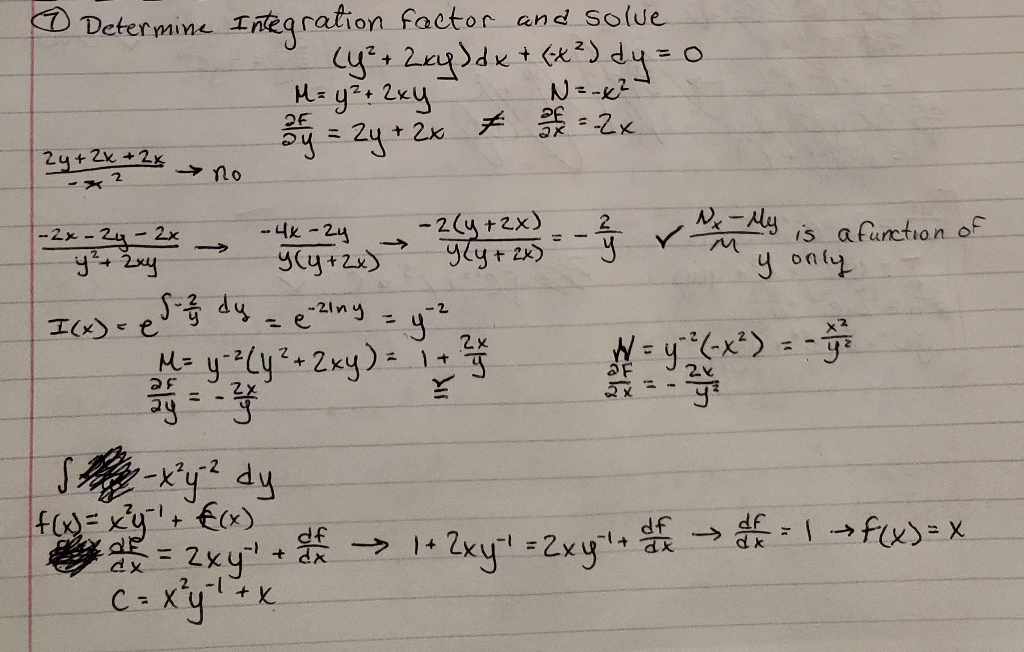Exact Differential Equation Integrating Factor - A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form. Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form.
Solved By finding an appropriate integrating factor, solve
We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Integrating factors • it is sometimes possible to convert a differential equation that is not.
Ex 9.6, 18 The integrating factor of differential equation
Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. We will see.
(PDF) The Integrating Factors of an Exact Differential Equation
Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. We will see.
Uses of Integrating Factor To Solve Non Exact Differential Equation
Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form. A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4}.
(PDF) Algorithm for Integrating Factor for a NonExact Linear First
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form. A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. Integrating.
Finding integrating factor for inexact differential equation
A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. We will see.
Integrating Factor Differential Equation All in one Photos
A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Integrating.
Integrating factor for a non exact differential form Mathematics
Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. We will see.
Solved ?Find an appropriate integrating factor for each
A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n. Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. We will see just what it means for a differential equation to be in exact form and how to solve differential equations in.
Solved Determine an integrating factor for the given
We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Integrating factors • it is sometimes possible to convert a differential equation that is not.
Some Equations That Are Not Exact May Be Multiplied By Some Factor, A Function U(X, Y), To Make Them Exact.
We will see just what it means for a differential equation to be in exact form and how to solve differential equations in this form. Integrating factors • it is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the. A function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n.