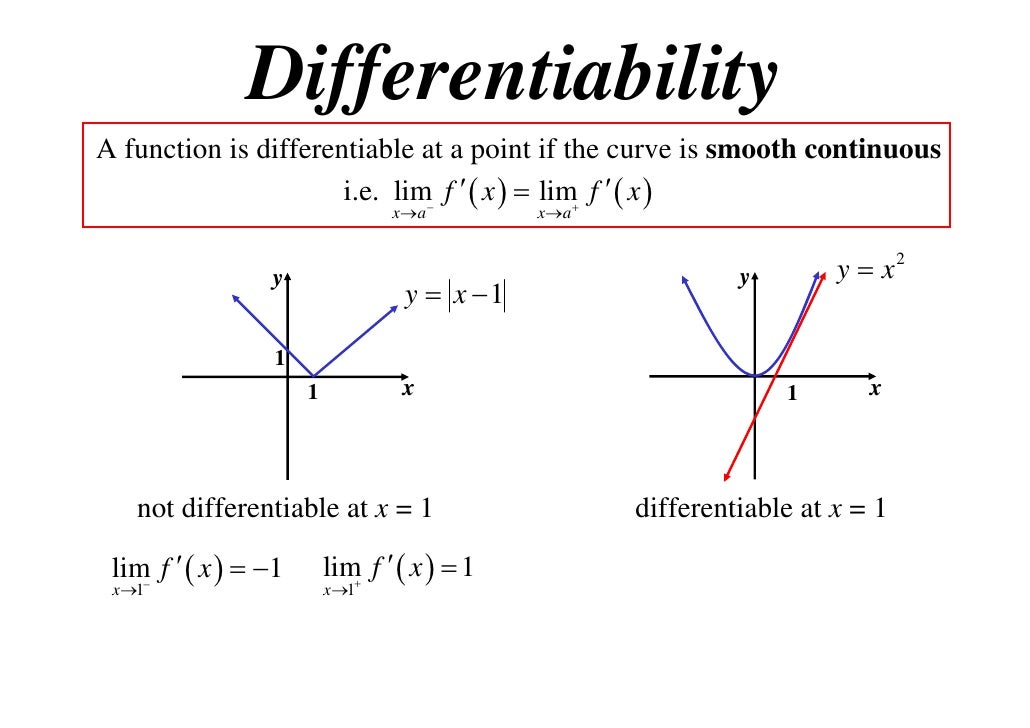
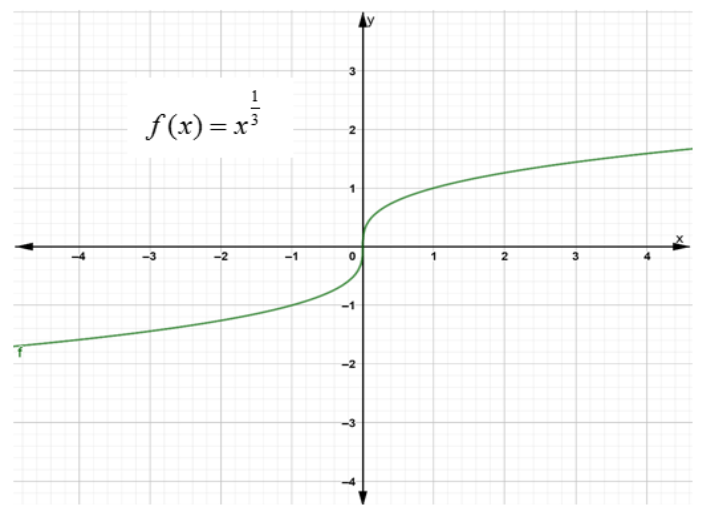
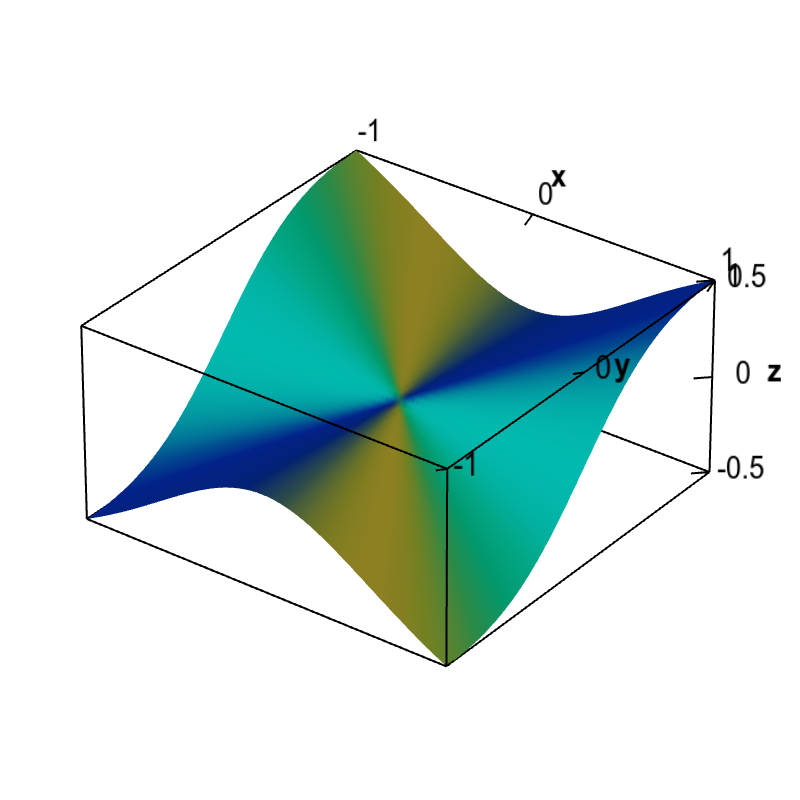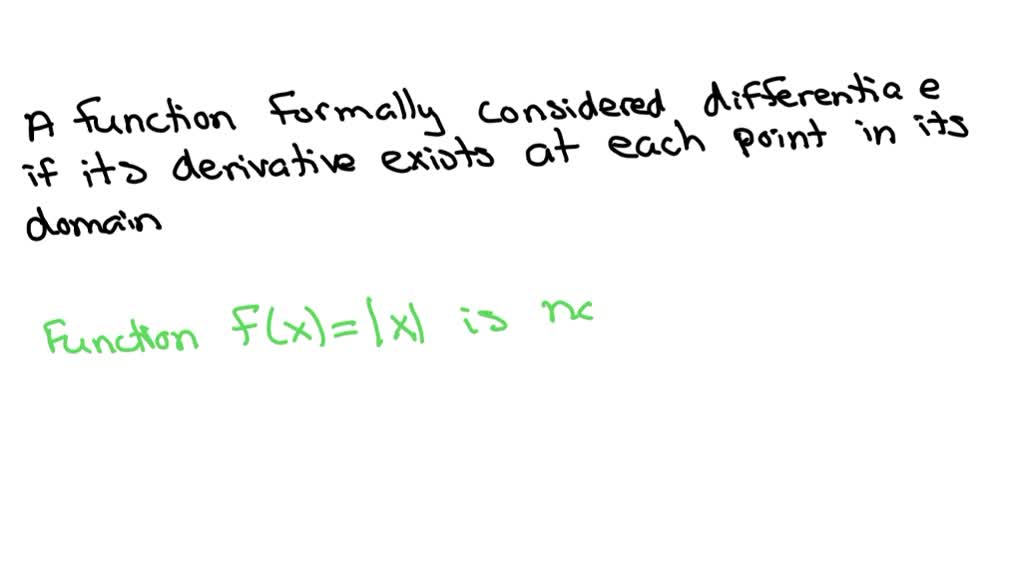Examples Of Not Differentiable - We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have a derivative at a point. The function jumps at x x, (is not continuous) like. For example, if there is a. When f is not continuous at x = x 0.
The function jumps at x x, (is not continuous) like. For example, if there is a. When f is not continuous at x = x 0. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have a derivative at a point.
When f is not continuous at x = x 0. Here are a number of cases in which f does not have a derivative at a point. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. The function jumps at x x, (is not continuous) like. For example, if there is a.
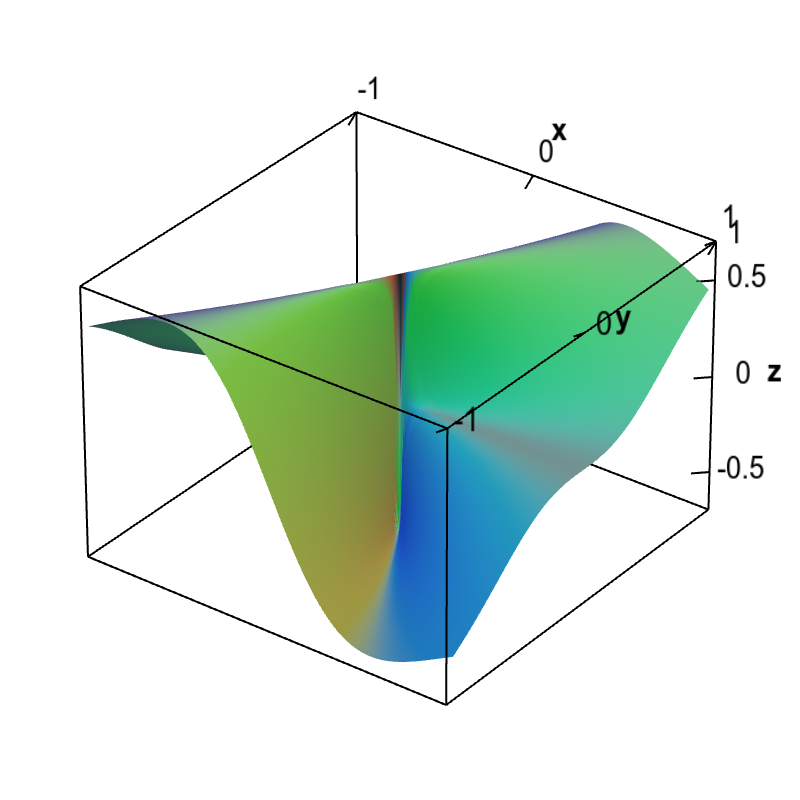
Nondifferentiable functions must have discontinuous partial
We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. For example, if there is a. The function jumps at x x, (is not continuous) like. When f is not continuous at x = x 0. Here are a number of cases.
Nondifferentiable functions must have discontinuous partial
For example, if there is a. The function jumps at x x, (is not continuous) like. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. When f is not continuous at x = x 0. Here are a number of cases.
When Is a Function Continuous but Not Differentiable Quant RL
We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. The function jumps at x x, (is not continuous) like. When f is not continuous at x = x 0. Here are a number of cases in which f does not have.
Can Something Be Differentiable but Not Continuous Quant RL
For example, if there is a. When f is not continuous at x = x 0. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have a derivative at a.
SOLVEDWrite a paragraph that explains what it means for a function to
We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have a derivative at a point. The function jumps at x x, (is not continuous) like. For example, if there is.
What are some examples of nondifferentiable functions?
We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. The function jumps at x x, (is not continuous) like. For example, if there is a. Here are a number of cases in which f does not have a derivative at a.
Differentiable Cuemath
Here are a number of cases in which f does not have a derivative at a point. The function jumps at x x, (is not continuous) like. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. When f is not continuous.
Differentiable Function Meaning, Formulas and Examples Outlier
We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have a derivative at a point. For example, if there is a. When f is not continuous at x = x.
Can Something Be Differentiable but Not Continuous Quant RL
The function jumps at x x, (is not continuous) like. When f is not continuous at x = x 0. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have.
Differentiable vs. Continuous Functions Understanding the Distinctions
For example, if there is a. Here are a number of cases in which f does not have a derivative at a point. The function jumps at x x, (is not continuous) like. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line.
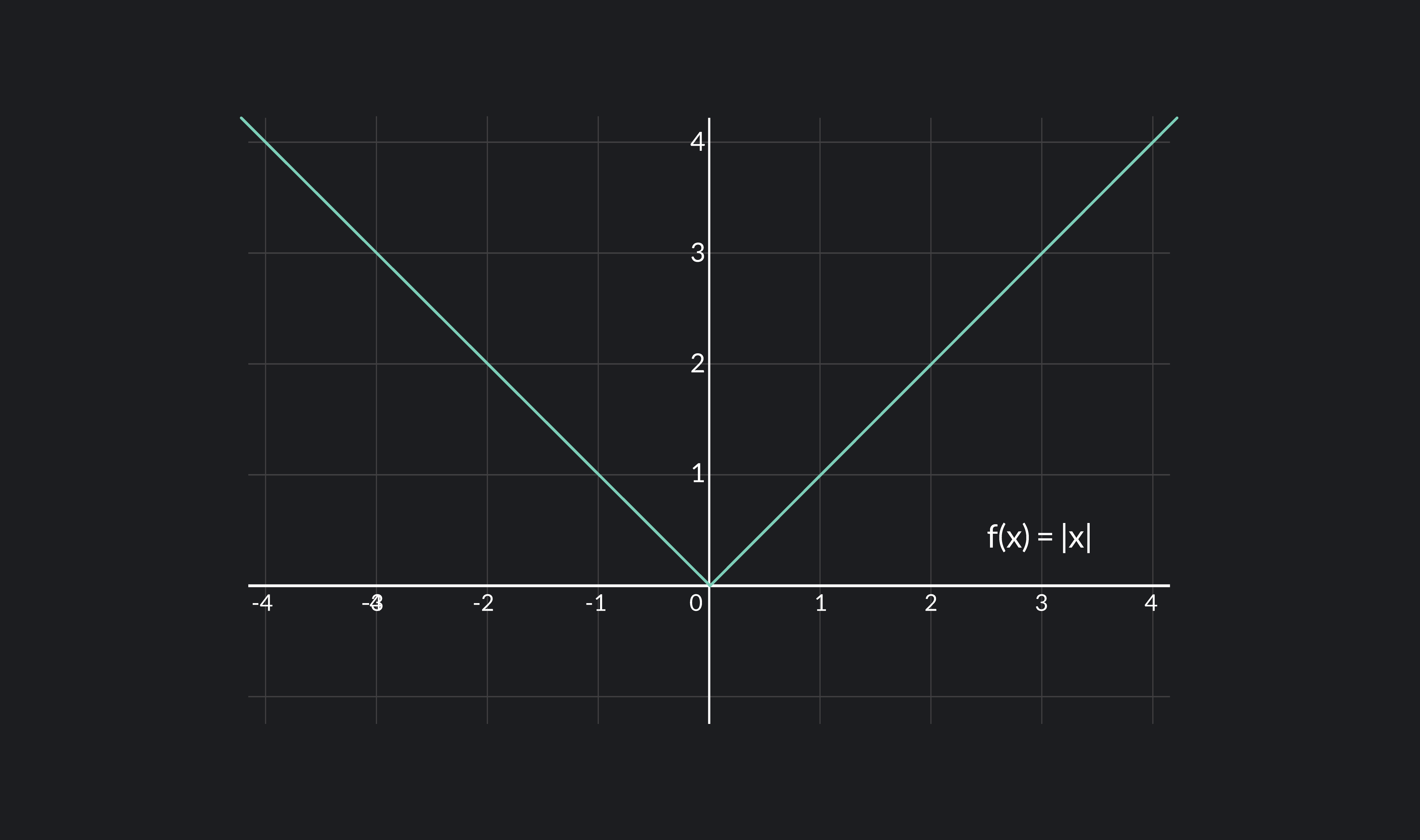
The Function Jumps At X X, (Is Not Continuous) Like.
For example, if there is a. Here are a number of cases in which f does not have a derivative at a point. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. When f is not continuous at x = x 0.