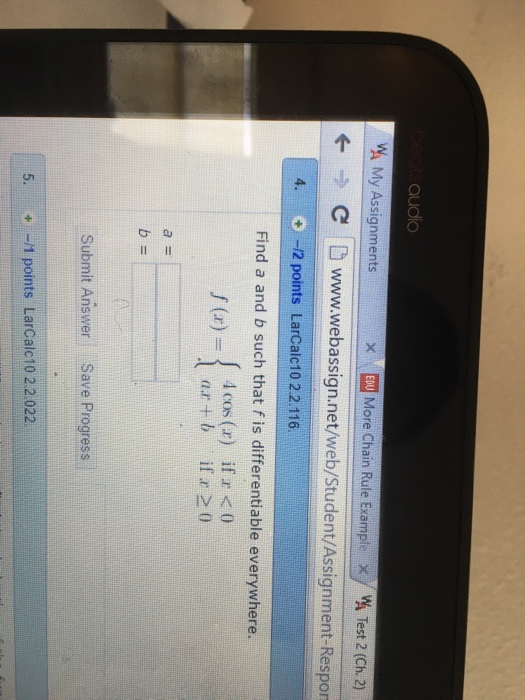
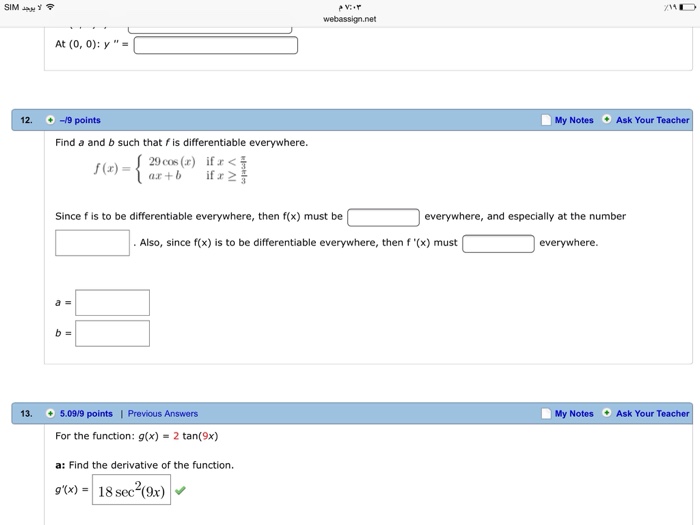
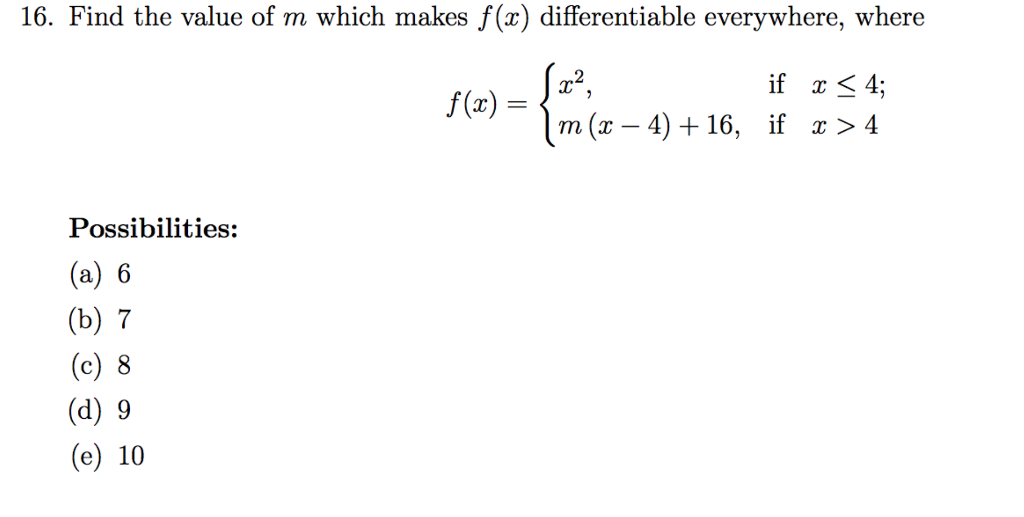Find A And B Such That F Is Differentiable Everywhere

Find A And B Such That F Is Differentiable Everywhere - F '(x) = acos(ax) then plug in x = 0 to get: F '(x) = acos(a(0)) = a•1 = a. To ensure that the function f(x) is. To make f differentiable everywhere, we set a = 0 and b can be any real number. $$(x^2+b)' = 2x+b$$ the correct way to get the value of $b$: There are 4 steps to solve this one. (a) find the values of a and b such that f(x) is differentiable everywhere and compute f′(x). Function $f(x)$ must be continuous at $x=2$. For f (x) to be differentiable everywhere, it must first be continuous everywhere. By equating the two parts of the piecewise function at the.

F(x) = sin(ax) + b. F '(x) = acos(a(0)) = a•1 = a. The values of a and b that make the function f differentiable everywhere are: Function $f(x)$ must be continuous at $x=2$. By equating the two parts of the piecewise function at the. To ensure that the function f(x) is. If and only if lim x → c − f (x) = lim x → c + f (x) =. For f (x) to be differentiable everywhere, it must first be continuous everywhere. Find a and b such that f is differentiable everywhere. Therefore, f(x) = 4 cos(x) for x < 0, and.

$$(x^2+b)' = 2x+b$$ the correct way to get the value of $b$: The values of a and b that make the function f differentiable everywhere are: F '(x) = acos(ax) then plug in x = 0 to get: F(x) = sin(ax) + b. By equating the two parts of the piecewise function at the. Function $f(x)$ must be continuous at $x=2$. (a) find the values of a and b such that f(x) is differentiable everywhere and compute f′(x). To make f differentiable everywhere, we set a = 0 and b can be any real number. To ensure that the function f(x) is. F '(x) = acos(a(0)) = a•1 = a.

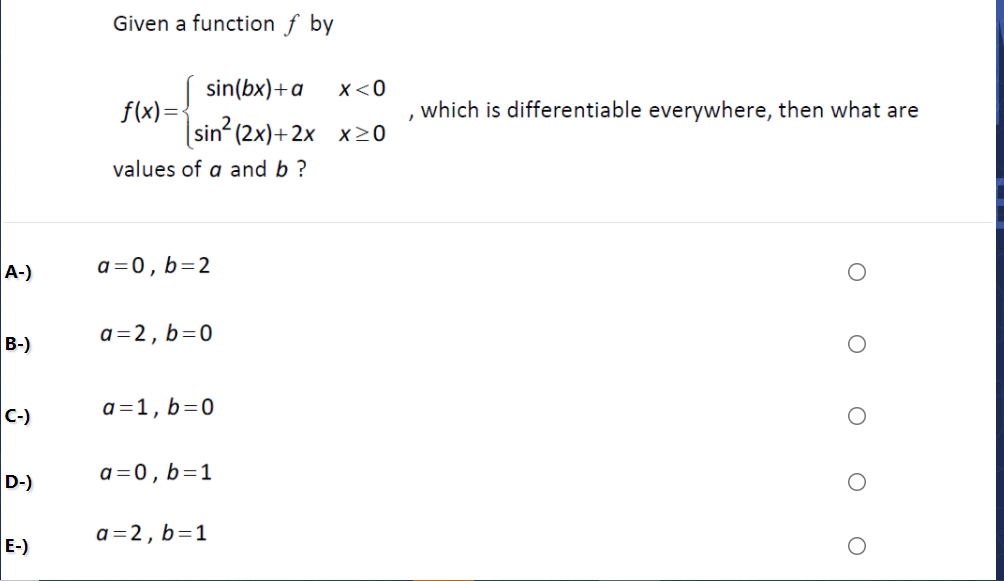
Solved Given a function f by which is differentiable

To make f differentiable everywhere, we set a = 0 and b can be any real number. By equating the two parts of the piecewise function at the. F '(x) = acos(ax) then plug in x = 0 to get: If and only if lim x → c − f (x) = lim x → c + f (x) =..

Solved Find a and b such that f is differentiable

Find all values of and that make the following. F(x) = sin(ax) + b. Therefore, f(x) = 4 cos(x) for x < 0, and. If and only if lim x → c − f (x) = lim x → c + f (x) =. To ensure that the function f(x) is.

Let f and g be differentiable on [0 , 1] such that f(0)=2 , g(0)=0, f(1

(b) is the function f ′ (x) differentiable. F '(x) = acos(ax) then plug in x = 0 to get: Find all values of and that make the following. Function $f(x)$ must be continuous at $x=2$. $$(x^2+b)' = 2x+b$$ the correct way to get the value of $b$:

Solved Find a and b such that f is differentiable

F '(x) = acos(ax) then plug in x = 0 to get: To make f differentiable everywhere, we set a = 0 and b can be any real number. By equating the two parts of the piecewise function at the. The values of a and b that make the function f differentiable everywhere are: F(x) = sin(ax) + b.

Solved 1. Assume f() is differentiable everywhere and has

F '(x) = acos(a(0)) = a•1 = a. (a) find the values of a and b such that f(x) is differentiable everywhere and compute f′(x). To ensure that the function f(x) is. There are 4 steps to solve this one. Therefore, f(x) = 4 cos(x) for x < 0, and.

Let f[0,1]→R is a differentiable function such that f(0) = 0 and f(x

Find all values of and that make the following. F '(x) = acos(ax) then plug in x = 0 to get: For f (x) to be differentiable everywhere, it must first be continuous everywhere. F(x) = sin(ax) + b. There are 4 steps to solve this one.

If f x is a twice differentiable function such that f a =0, f b =2, f c

There are 4 steps to solve this one. Find a and b such that f is differentiable everywhere. Therefore, f(x) = 4 cos(x) for x < 0, and. The values of a and b that make the function f differentiable everywhere are: For f (x) to be differentiable everywhere, it must first be continuous everywhere.

Solved Find the Values of m and b that make f(x)

By equating the two parts of the piecewise function at the. There are 4 steps to solve this one. Function $f(x)$ must be continuous at $x=2$. To ensure that the function f(x) is. (b) is the function f ′ (x) differentiable.

Solved Find a and b such that f is differentiable

To make f differentiable everywhere, we set a = 0 and b can be any real number. F(x) = sin(ax) + b. There are 4 steps to solve this one. (a) find the values of a and b such that f(x) is differentiable everywhere and compute f′(x). Find all values of and that make the following.

Solved Find the value of m which makes f (x) differentiable

For f (x) to be differentiable everywhere, it must first be continuous everywhere. Therefore, f(x) = 4 cos(x) for x < 0, and. If and only if lim x → c − f (x) = lim x → c + f (x) =. F '(x) = acos(ax) then plug in x = 0 to get: F '(x) = acos(a(0)) =.

For F (X) To Be Differentiable Everywhere, It Must First Be Continuous Everywhere.

(b) is the function f ′ (x) differentiable. F '(x) = acos(a(0)) = a•1 = a. If and only if lim x → c − f (x) = lim x → c + f (x) =. $$(x^2+b)' = 2x+b$$ the correct way to get the value of $b$:

Function $F(X)$ Must Be Continuous At $X=2$.

F '(x) = acos(ax) then plug in x = 0 to get: To make f differentiable everywhere, we set a = 0 and b can be any real number. Therefore, f(x) = 4 cos(x) for x < 0, and. Find all values of and that make the following.

By Equating The Two Parts Of The Piecewise Function At The.

The values of a and b that make the function f differentiable everywhere are: (a) find the values of a and b such that f(x) is differentiable everywhere and compute f′(x). To ensure that the function f(x) is. Find a and b such that f is differentiable everywhere.