How To Find Differentials - Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. How are dy, dx and δ y and δ x related? We are introducing differentials here as an introduction to the notation used in integration. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do.
How are dy, dx and δ y and δ x related? For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. We are introducing differentials here as an introduction to the notation used in integration. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy.
Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. How are dy, dx and δ y and δ x related? We are introducing differentials here as an introduction to the notation used in integration.
Misc 1 Using differentials, find approximate value 17/81
We are introducing differentials here as an introduction to the notation used in integration. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. How are dy, dx and δ y and δ x related? Given a function \(y = f\left( x \right)\) we call \(dy\).
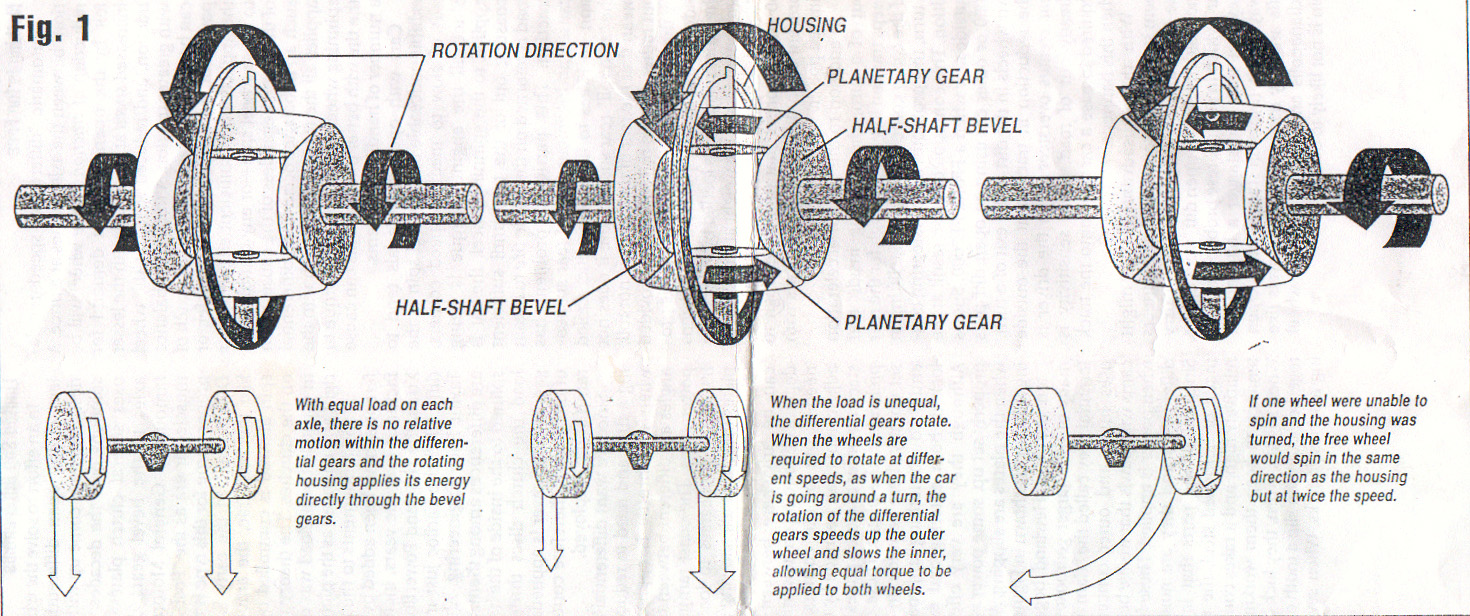
Detail Tech Guide Differentials Drive
We are introducing differentials here as an introduction to the notation used in integration. How are dy, dx and δ y and δ x related? Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential.
ShowMe differentials
How are dy, dx and δ y and δ x related? For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. We are introducing differentials here as an introduction to the notation used in integration. Given a function \(y = f\left( x \right)\) we call \(dy\).
Misc 1 Using differentials, find approximate value 17/81
How are dy, dx and δ y and δ x related? We are introducing differentials here as an introduction to the notation used in integration. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential.
Misc 1 Using differentials, find approximate value 17/81
We are introducing differentials here as an introduction to the notation used in integration. How are dy, dx and δ y and δ x related? Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential.
Rocky Mountain Healey Club Differentials
Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. We are introducing differentials here as an introduction to the notation used in integration. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s.
Question 1 (a) Using differentials, find approximate value of (17/81
How are dy, dx and δ y and δ x related? We are introducing differentials here as an introduction to the notation used in integration. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential.
Question 1 (a) Using differentials, find approximate value of (17/81
We are introducing differentials here as an introduction to the notation used in integration. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. How are dy, dx and δ y and δ x related? Given a function \(y = f\left( x \right)\) we call \(dy\).
Separable differential equations 2 JustToThePoint
We are introducing differentials here as an introduction to the notation used in integration. How are dy, dx and δ y and δ x related? Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential.
Get the Most Out of Your Car Understanding Rear Differentials Care
How are dy, dx and δ y and δ x related? Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. We are introducing differentials here as an introduction to the notation used in integration. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential.
We Are Introducing Differentials Here As An Introduction To The Notation Used In Integration.
How are dy, dx and δ y and δ x related? Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do.