How To Find The Differential - In this kind of problem we’re being asked to compute the differential of the function. Calculate the relative error and percentage error in using a differential. When we first looked at derivatives, we used the leibniz. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. Draw a graph that illustrates the use of differentials to approximate the change in a quantity. There is a natural extension to functions of three or more variables. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values.
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. There is a natural extension to functions of three or more variables. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). Draw a graph that illustrates the use of differentials to approximate the change in a quantity. Calculate the relative error and percentage error in using a differential. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] In this kind of problem we’re being asked to compute the differential of the function. When we first looked at derivatives, we used the leibniz. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values.
Draw a graph that illustrates the use of differentials to approximate the change in a quantity. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. When we first looked at derivatives, we used the leibniz. In this kind of problem we’re being asked to compute the differential of the function. Calculate the relative error and percentage error in using a differential. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. There is a natural extension to functions of three or more variables. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\]
[Solved] solve the partial differential equation by finding the
Draw a graph that illustrates the use of differentials to approximate the change in a quantity. In this kind of problem we’re being asked to compute the differential of the function. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). Calculate the relative error and percentage error in using a differential..
coordinate systems How is Cartesian differential equation converted
Calculate the relative error and percentage error in using a differential. When we first looked at derivatives, we used the leibniz. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. In this kind of problem we’re being asked to compute the differential of the function. In.
Application of Differential Equation
In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. When we first looked at derivatives, we used the leibniz. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). Differentials provide us with a way of estimating the amount a function changes as.
Differential Equation Calculator Examples, Facts
Draw a graph that illustrates the use of differentials to approximate the change in a quantity. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. When we first.
Android İndirme için Find Differential Detectives APK
When we first looked at derivatives, we used the leibniz. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] In this kind of problem we’re being asked to compute the differential of the function. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. The differential.
Differential Equations (Definition, Types, Order, Degree, Examples)
In this kind of problem we’re being asked to compute the differential of the function. When we first looked at derivatives, we used the leibniz. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually.
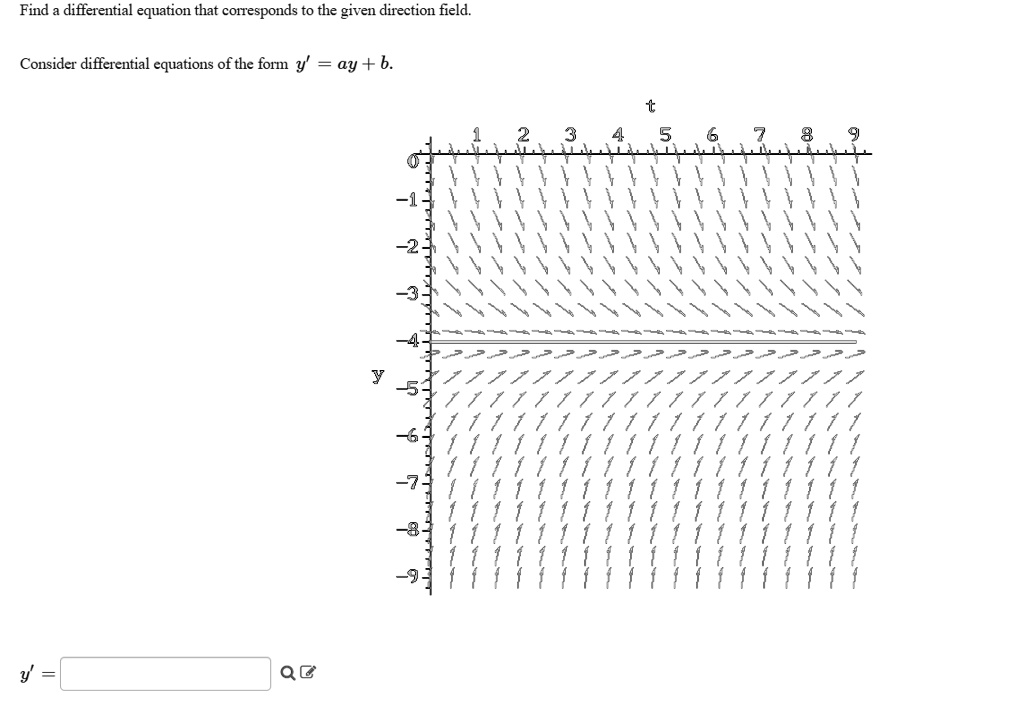
find differential equation that corresponds to the given direction
In this kind of problem we’re being asked to compute the differential of the function. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw =.
Particular Solution of NonHomogeneous Differential Equations Mr
When we first looked at derivatives, we used the leibniz. Calculate the relative error and percentage error in using a differential. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. There is a natural extension to functions of three or more variables. In other words, \(dy\) for the first problem,.
PPT DIFFERENTIAL EQUATIONS PowerPoint Presentation, free download
Calculate the relative error and percentage error in using a differential. In this kind of problem we’re being asked to compute the differential of the function. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] When we first looked at derivatives, we used the leibniz. Differentials provide us with a way of estimating the amount a function changes as.
[Solved] Find the general solution of the following differential
In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. When we first looked at derivatives, we used the leibniz. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. Calculate the relative error and percentage error in using a differential. Differentials provide.
The Differential Of \(X\), Denoted \(Dx\), Is Any Nonzero Real Number (Usually Taken To Be A Small Number).
Draw a graph that illustrates the use of differentials to approximate the change in a quantity. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] There is a natural extension to functions of three or more variables. In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third.
Differentials Provide Us With A Way Of Estimating The Amount A Function Changes As A Result Of A Small Change In Input Values.
When we first looked at derivatives, we used the leibniz. Calculate the relative error and percentage error in using a differential. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. In this kind of problem we’re being asked to compute the differential of the function.