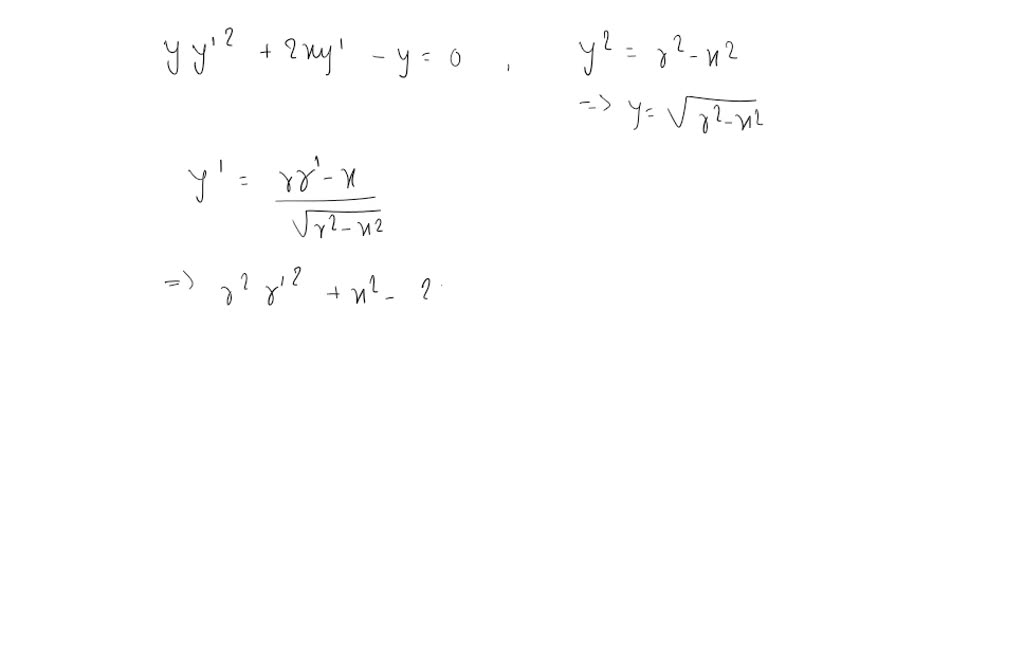How To Prove A Differential Equation Is Homogeneous - A differential equation can be homogeneous in either of two respects. The best and the simplest test for checking the homogeneity of a differential. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both.
The best and the simplest test for checking the homogeneity of a differential. A differential equation can be homogeneous in either of two respects. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both.
A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both. The best and the simplest test for checking the homogeneity of a differential. A differential equation can be homogeneous in either of two respects.
please derive the homogeneous differential equation of this question
A differential equation can be homogeneous in either of two respects. The best and the simplest test for checking the homogeneity of a differential. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both.
Solution of Homogeneous Linear Differential equation Yawin
A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both. A differential equation can be homogeneous in either of two respects. The best and the simplest test for checking the homogeneity of a differential.
3. Differential Equation Homogeneous Differential Lecture.2024.pptx
A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both. A differential equation can be homogeneous in either of two respects. The best and the simplest test for checking the homogeneity of a differential.
SOLUTION Homogeneous differential equation Studypool
A differential equation can be homogeneous in either of two respects. The best and the simplest test for checking the homogeneity of a differential. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both.
3. Differential Equation Homogeneous Differential Lecture.2024.pptx
The best and the simplest test for checking the homogeneity of a differential. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both. A differential equation can be homogeneous in either of two respects.
SOLUTION Homogeneous differential equation Studypool
A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both. A differential equation can be homogeneous in either of two respects. The best and the simplest test for checking the homogeneity of a differential.
SOLVED Prove that if a homogeneous firstorder differential equation
The best and the simplest test for checking the homogeneity of a differential. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both. A differential equation can be homogeneous in either of two respects.
Homogeneous Differential Equation Know types, Steps to solve
A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both. The best and the simplest test for checking the homogeneity of a differential. A differential equation can be homogeneous in either of two respects.
[Solved] Solve the HOMOGENEOUS differential equation in step by step
The best and the simplest test for checking the homogeneity of a differential. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both. A differential equation can be homogeneous in either of two respects.
SOLUTION Chapter 4 homogeneous differential equation Studypool
A differential equation can be homogeneous in either of two respects. The best and the simplest test for checking the homogeneity of a differential. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both.
The Best And The Simplest Test For Checking The Homogeneity Of A Differential.
A differential equation can be homogeneous in either of two respects. A first‐order differential equation is said to be homogeneous if m( x,y) and n( x,y) are both.