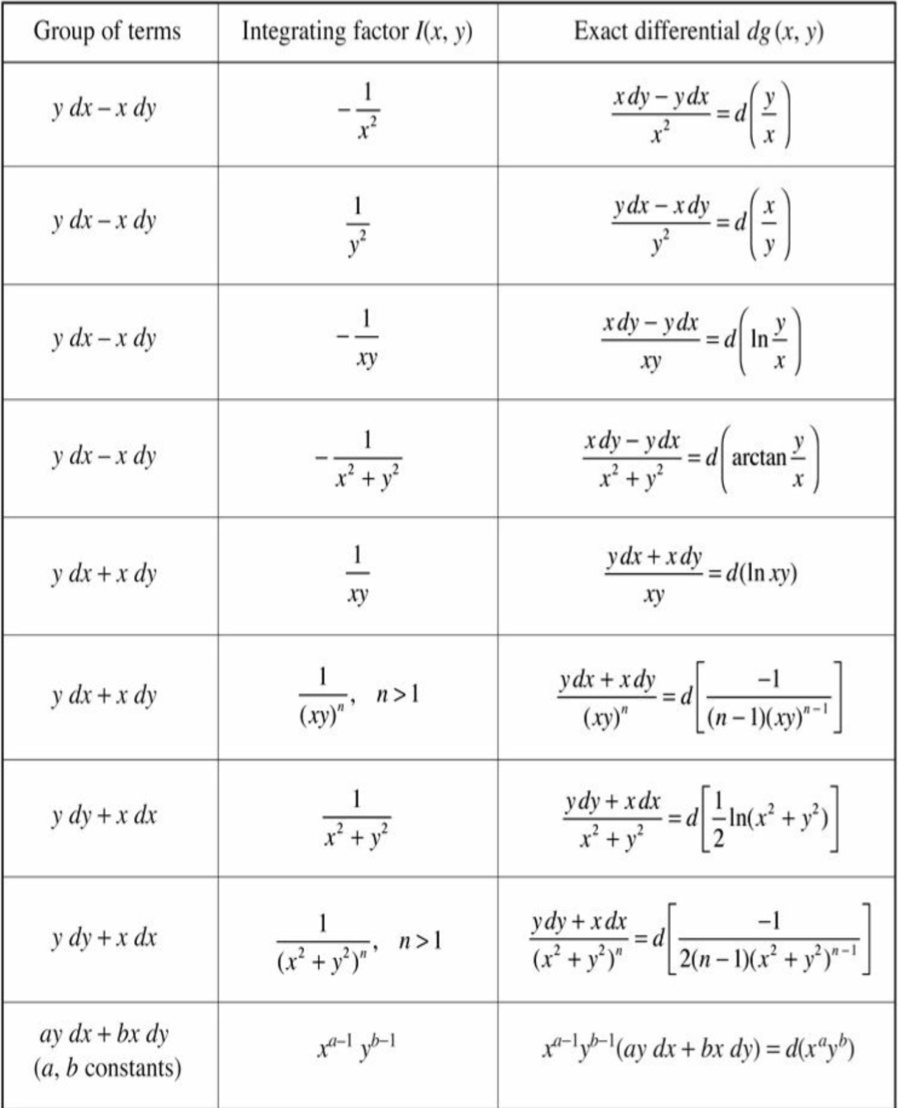
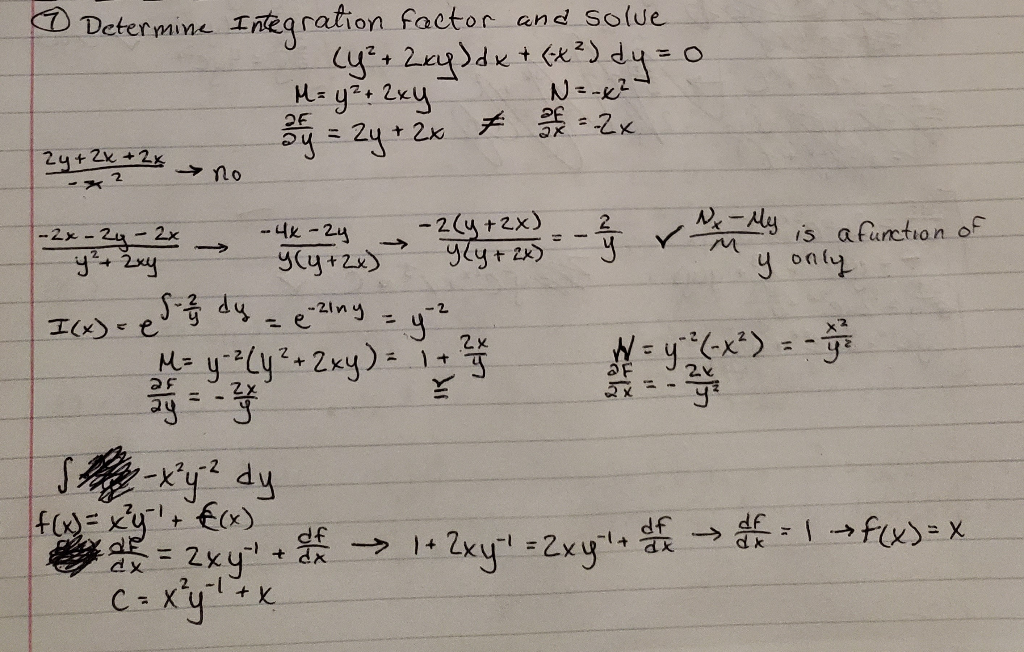Integrating A Differential Equation - Dy dx +p(x)y = q(x) has the integrating factor if=e r. All equations with derivatives of a variable w.r.t. The linear first order differential equation: Integrating factor is defined as the function which is selected in order to solve the given. Another are called 'differential equations'. An ordinary differential equation of the following form: Dy dx = f(x) can be solved by integrating. Learn how to use integration in higher maths to solve differential equations and find the area. Let us now briefly consider the general case where integration is immediately applicable, and also.
Another are called 'differential equations'. An ordinary differential equation of the following form: Learn how to use integration in higher maths to solve differential equations and find the area. Let us now briefly consider the general case where integration is immediately applicable, and also. Dy dx = f(x) can be solved by integrating. Integrating factor is defined as the function which is selected in order to solve the given. All equations with derivatives of a variable w.r.t. Dy dx +p(x)y = q(x) has the integrating factor if=e r. The linear first order differential equation:
Let us now briefly consider the general case where integration is immediately applicable, and also. Dy dx = f(x) can be solved by integrating. Dy dx +p(x)y = q(x) has the integrating factor if=e r. Integrating factor is defined as the function which is selected in order to solve the given. All equations with derivatives of a variable w.r.t. The linear first order differential equation: An ordinary differential equation of the following form: Learn how to use integration in higher maths to solve differential equations and find the area. Another are called 'differential equations'.
Uses of Integrating Factor To Solve Non Exact Differential Equation
Dy dx +p(x)y = q(x) has the integrating factor if=e r. Another are called 'differential equations'. An ordinary differential equation of the following form: Dy dx = f(x) can be solved by integrating. The linear first order differential equation:
Integrating Factor Differential Equation All in one Photos
All equations with derivatives of a variable w.r.t. Integrating factor is defined as the function which is selected in order to solve the given. Dy dx +p(x)y = q(x) has the integrating factor if=e r. Let us now briefly consider the general case where integration is immediately applicable, and also. Dy dx = f(x) can be solved by integrating.
Solved 1. Integrating Factor. Find the general solution to
Integrating factor is defined as the function which is selected in order to solve the given. Dy dx = f(x) can be solved by integrating. An ordinary differential equation of the following form: Dy dx +p(x)y = q(x) has the integrating factor if=e r. The linear first order differential equation:
Solved Determine an integrating factor for the given
Integrating factor is defined as the function which is selected in order to solve the given. Dy dx +p(x)y = q(x) has the integrating factor if=e r. All equations with derivatives of a variable w.r.t. Another are called 'differential equations'. Learn how to use integration in higher maths to solve differential equations and find the area.
Finding integrating factor for inexact differential equation
Let us now briefly consider the general case where integration is immediately applicable, and also. Learn how to use integration in higher maths to solve differential equations and find the area. An ordinary differential equation of the following form: Dy dx +p(x)y = q(x) has the integrating factor if=e r. Dy dx = f(x) can be solved by integrating.
Solved ?Find an appropriate integrating factor for each
Integrating factor is defined as the function which is selected in order to solve the given. Learn how to use integration in higher maths to solve differential equations and find the area. An ordinary differential equation of the following form: Let us now briefly consider the general case where integration is immediately applicable, and also. Dy dx = f(x) can.
5) Integrating factor of differential equation (tan y Math
An ordinary differential equation of the following form: All equations with derivatives of a variable w.r.t. Another are called 'differential equations'. Dy dx = f(x) can be solved by integrating. Learn how to use integration in higher maths to solve differential equations and find the area.
integrating factor of the differential equation X dy/dxy = 2 x ^2 is A
Another are called 'differential equations'. The linear first order differential equation: Learn how to use integration in higher maths to solve differential equations and find the area. An ordinary differential equation of the following form: Let us now briefly consider the general case where integration is immediately applicable, and also.
Ex 9.6, 18 The integrating factor of differential equation
Dy dx +p(x)y = q(x) has the integrating factor if=e r. Another are called 'differential equations'. An ordinary differential equation of the following form: All equations with derivatives of a variable w.r.t. Learn how to use integration in higher maths to solve differential equations and find the area.
(PDF) The Integrating Factors of an Exact Differential Equation
Dy dx +p(x)y = q(x) has the integrating factor if=e r. Let us now briefly consider the general case where integration is immediately applicable, and also. All equations with derivatives of a variable w.r.t. Integrating factor is defined as the function which is selected in order to solve the given. An ordinary differential equation of the following form:
An Ordinary Differential Equation Of The Following Form:
The linear first order differential equation: Dy dx +p(x)y = q(x) has the integrating factor if=e r. Integrating factor is defined as the function which is selected in order to solve the given. All equations with derivatives of a variable w.r.t.
Learn How To Use Integration In Higher Maths To Solve Differential Equations And Find The Area.
Another are called 'differential equations'. Dy dx = f(x) can be solved by integrating. Let us now briefly consider the general case where integration is immediately applicable, and also.