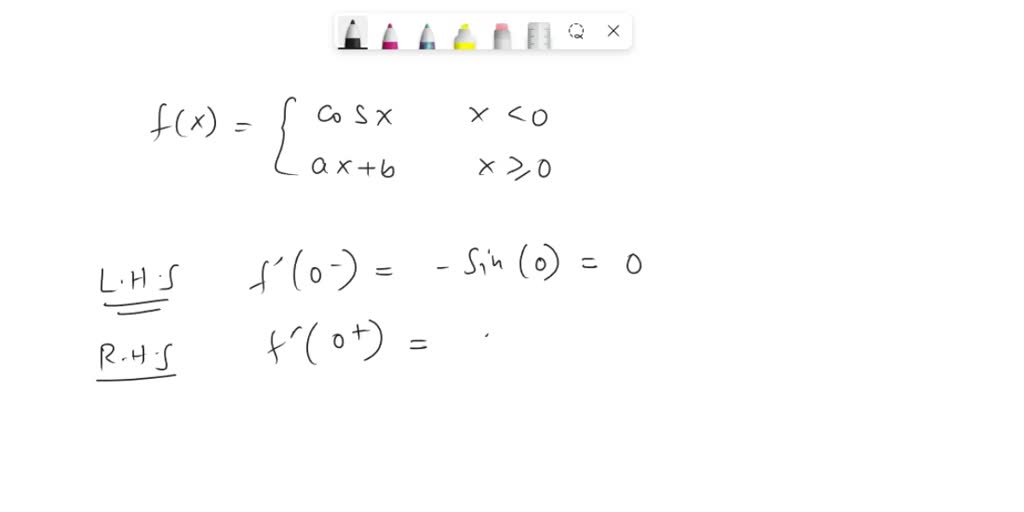Is Cos X Differentiable Everywhere - If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that f is not differentiable at x = 1. From the graph of $|\cos x|$, we can see that the $|\cos x|$ is differentiable. Thus, for the question of whether $\cos(|x|)$ or $\sin(|x|)$ is differentiable at. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not. Determine whether \[f\left( x \right) = \binom{\frac{\sin x^2}{x}, x \neq 0}{0, x = 0}\] is. The function f (x) = |cos x| is (a) everywhere continuous and differentiable (b) everywhere.
Thus, for the question of whether $\cos(|x|)$ or $\sin(|x|)$ is differentiable at. If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that f is not differentiable at x = 1. From the graph of $|\cos x|$, we can see that the $|\cos x|$ is differentiable. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). The function f (x) = |cos x| is (a) everywhere continuous and differentiable (b) everywhere. Determine whether \[f\left( x \right) = \binom{\frac{\sin x^2}{x}, x \neq 0}{0, x = 0}\] is. The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not.
The function f (x) = |cos x| is (a) everywhere continuous and differentiable (b) everywhere. The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not. From the graph of $|\cos x|$, we can see that the $|\cos x|$ is differentiable. If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that f is not differentiable at x = 1. Determine whether \[f\left( x \right) = \binom{\frac{\sin x^2}{x}, x \neq 0}{0, x = 0}\] is. Thus, for the question of whether $\cos(|x|)$ or $\sin(|x|)$ is differentiable at. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1).
calculus Why isn't f(x) = x\cos\frac{\pi}{x} differentiable at x=0
From the graph of $|\cos x|$, we can see that the $|\cos x|$ is differentiable. If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that f is not differentiable at x = 1. The function f (x) = |cos x| is (a) everywhere continuous and differentiable (b) everywhere. I got the answer to be everywhere.
x is differentiable at x = 0 Maths Questions
The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). Determine whether \[f\left( x \right) = \binom{\frac{\sin x^2}{x}, x \neq 0}{0, x = 0}\] is. The function f (x) = |cos x| is (a) everywhere continuous and.
cos x is differentiable everywhere.
If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that f is not differentiable at x = 1. Determine whether \[f\left( x \right) = \binom{\frac{\sin x^2}{x}, x \neq 0}{0, x = 0}\] is. Thus, for the question of whether $\cos(|x|)$ or $\sin(|x|)$ is differentiable at. From the graph of $|\cos x|$, we can see that.
calculus Is f(x)=xx differentiable everywhere? Mathematics
Thus, for the question of whether $\cos(|x|)$ or $\sin(|x|)$ is differentiable at. The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). The function f (x) = |cos x| is (a) everywhere continuous and differentiable (b) everywhere..
The function fx=cos 14 x3 3 x isA. always differentiableB. not
The function f (x) = |cos x| is (a) everywhere continuous and differentiable (b) everywhere. The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`,.
Solved Let g be an everywhere differentiable function, such
Thus, for the question of whether $\cos(|x|)$ or $\sin(|x|)$ is differentiable at. The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that.
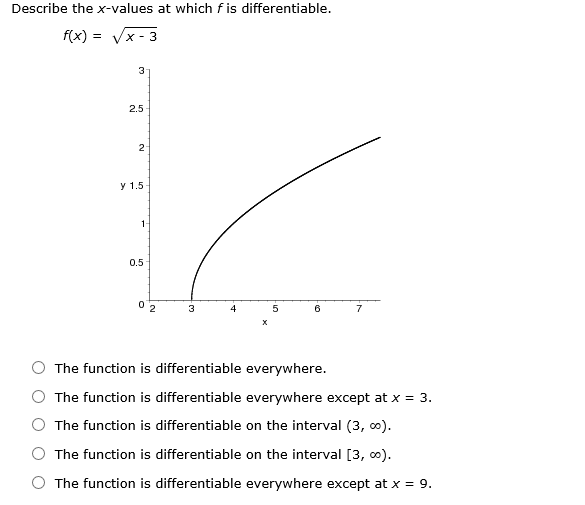
Solved Describe the xvalues at which f is differentiable.
From the graph of $|\cos x|$, we can see that the $|\cos x|$ is differentiable. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not. The function f (x) = |cos x| is (a) everywhere continuous and.
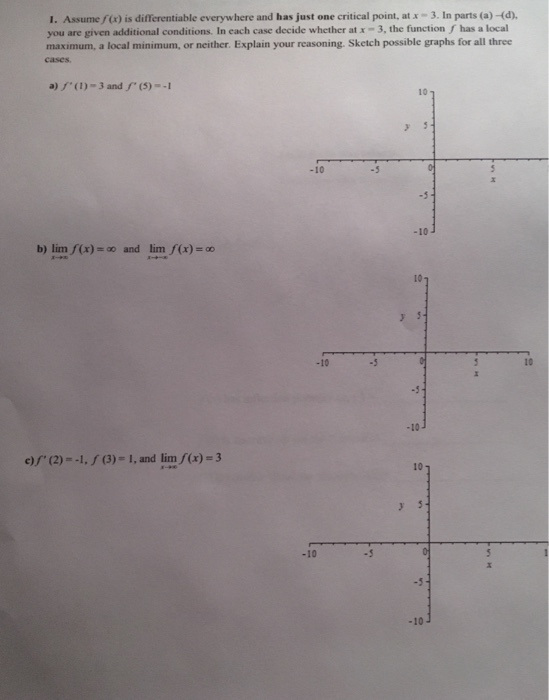
Solved 1. Assume f() is differentiable everywhere and has
If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that f is not differentiable at x = 1. The function f (x) = |cos x| is (a) everywhere continuous and differentiable (b) everywhere. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). Thus, for the question of whether $\cos(|x|)$ or.
Solved Suppose that f(x) = xπcos(x) is differentiable and
From the graph of $|\cos x|$, we can see that the $|\cos x|$ is differentiable. Determine whether \[f\left( x \right) = \binom{\frac{\sin x^2}{x}, x \neq 0}{0, x = 0}\] is. The function f (x) = |cos x| is (a) everywhere continuous and differentiable (b) everywhere. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1). The.
SOLVED Find 'a' and 'b' such that f is differentiable everywhere f(x
Thus, for the question of whether $\cos(|x|)$ or $\sin(|x|)$ is differentiable at. If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that f is not differentiable at x = 1. The function f (x) = 1 + |cos x| is (a) continuous no where (b) continuous everywhere (c) not. From the graph of $|\cos x|$,.
The Function F (X) = |Cos X| Is (A) Everywhere Continuous And Differentiable (B) Everywhere.
If f(x) = `{{:(x^2, if x ≥ 1),(x, if x < 1):}`, then show that f is not differentiable at x = 1. Determine whether \[f\left( x \right) = \binom{\frac{\sin x^2}{x}, x \neq 0}{0, x = 0}\] is. Thus, for the question of whether $\cos(|x|)$ or $\sin(|x|)$ is differentiable at. I got the answer to be everywhere continuous and not differentiable at $ x=(2n+1).
The Function F (X) = 1 + |Cos X| Is (A) Continuous No Where (B) Continuous Everywhere (C) Not.
From the graph of $|\cos x|$, we can see that the $|\cos x|$ is differentiable.