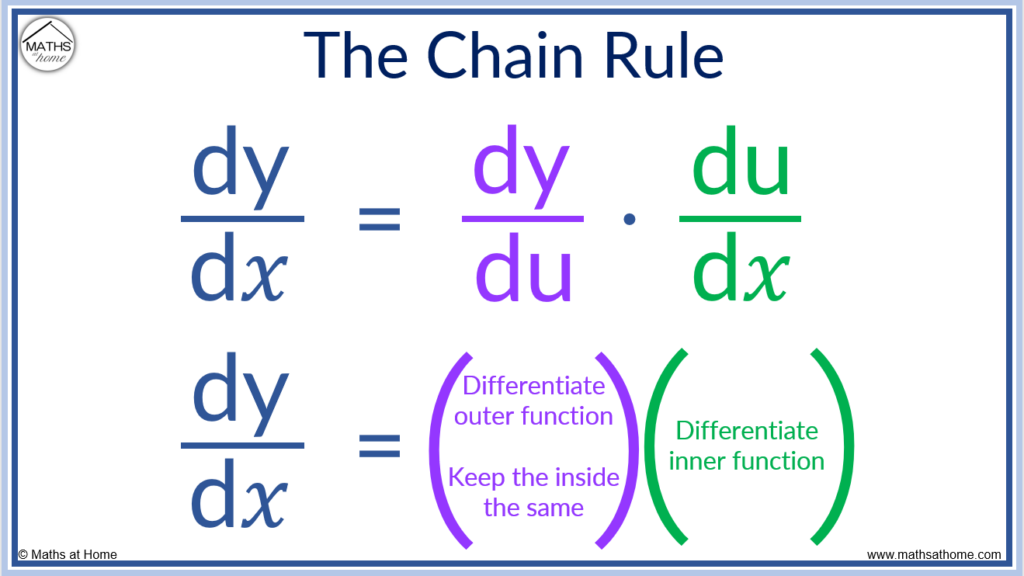
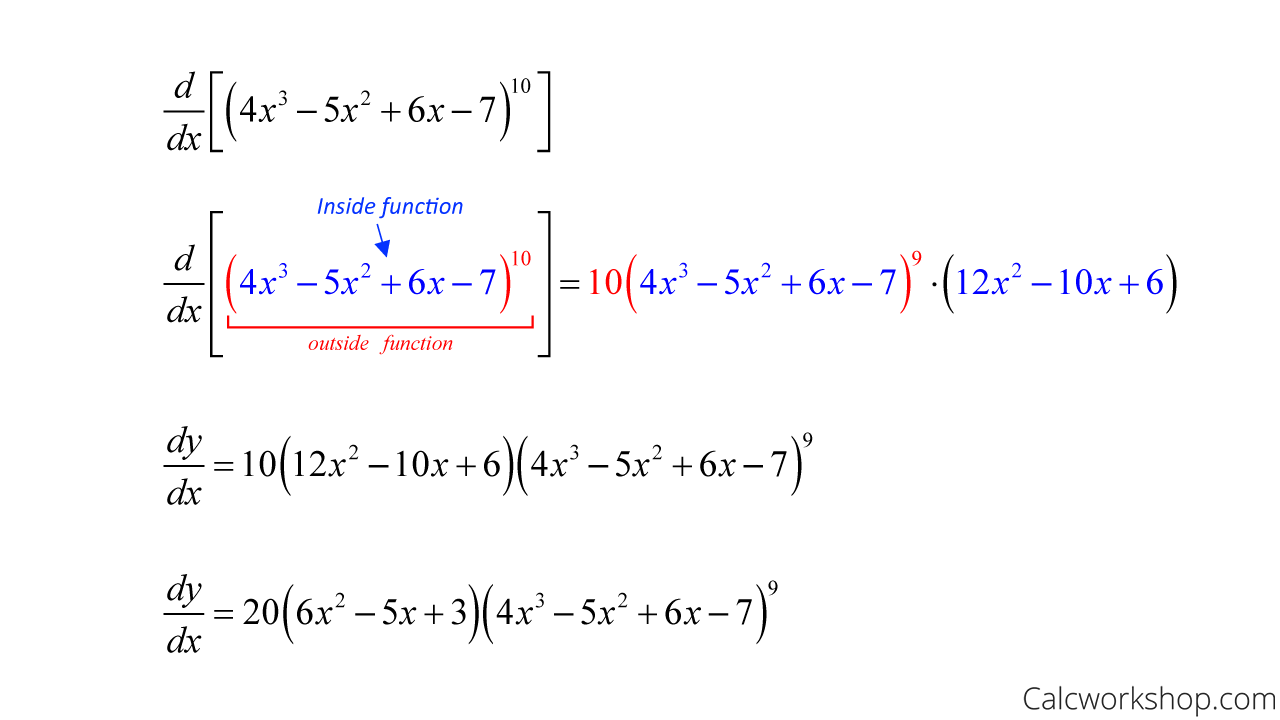Matrix Differentiation Chain Rule - Use the chain rule to find relations between different partial derivatives of a function. My problem is computing $\frac{\partial h}{\partial w_1}$. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. Denote also g(a) = [gij(a)], a = [aij], c = [cij]. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. Rk × k → rn × n as a(b) = c ′ bc.
The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. Use the chain rule to find relations between different partial derivatives of a function. Denote also g(a) = [gij(a)], a = [aij], c = [cij]. Rk × k → rn × n as a(b) = c ′ bc. My problem is computing $\frac{\partial h}{\partial w_1}$. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point.
Rk × k → rn × n as a(b) = c ′ bc. Use the chain rule to find relations between different partial derivatives of a function. My problem is computing $\frac{\partial h}{\partial w_1}$. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. Denote also g(a) = [gij(a)], a = [aij], c = [cij]. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point.
The Chain Rule Made Easy Examples and Solutions
My problem is computing $\frac{\partial h}{\partial w_1}$. Use the chain rule to find relations between different partial derivatives of a function. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. Rk × k → rn × n as a(b) = c ′ bc. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine.
The Chain Rule Made Easy Examples and Solutions
The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. Denote also g(a) = [gij(a)], a = [aij], c = [cij]. Rk × k → rn × n as a(b) = c ′ bc. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. Use the chain.
calculus Automatic Differentiation Chain Rule Question
My problem is computing $\frac{\partial h}{\partial w_1}$. Denote also g(a) = [gij(a)], a = [aij], c = [cij]. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. Rk × k → rn × n as a(b) = c ′ bc. Use the chain rule to find relations between different partial derivatives of a.
Formula of Differentiation by chain rule With solved example
Rk × k → rn × n as a(b) = c ′ bc. My problem is computing $\frac{\partial h}{\partial w_1}$. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. The purpose of this document is to help.
Lecture 2 Continue Intro Diff and Chain Rule PDF
The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. My problem is computing $\frac{\partial h}{\partial w_1}$. Denote also g(a) = [gij(a)], a = [aij], c = [cij]. Rk × k → rn × n as a(b) =.
The Chain Rule Made Easy Examples and Solutions
Rk × k → rn × n as a(b) = c ′ bc. Denote also g(a) = [gij(a)], a = [aij], c = [cij]. Use the chain rule to find relations between different partial derivatives of a function. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. My problem is computing $\frac{\partial.
M53 Lec2.2 The Chain Rule and Differentiability PDF
Use the chain rule to find relations between different partial derivatives of a function. Rk × k → rn × n as a(b) = c ′ bc. My problem is computing $\frac{\partial h}{\partial w_1}$. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. The purpose of this document is to help you learn.
14.5 The Chain Rule PDF Derivative Function (Mathematics)
Denote also g(a) = [gij(a)], a = [aij], c = [cij]. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. My problem is computing $\frac{\partial h}{\partial w_1}$. Rk × k → rn × n as a(b) = c ′ bc. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix.
Chain Rule Applications of Chain Rule PDF Subtraction Syntax (Logic)
The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. My problem is computing $\frac{\partial h}{\partial w_1}$. Rk × k → rn × n as a(b) = c ′ bc. Use the chain rule to find relations between different partial derivatives of a function. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine.
Chain Rule Differentiation Benytr
The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. Rk × k → rn × n as a(b) = c ′ bc. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point. Use the chain rule to find relations between different partial derivatives of a function. Denote.
Denote Also G(A) = [Gij(A)], A = [Aij], C = [Cij].
Use the chain rule to find relations between different partial derivatives of a function. My problem is computing $\frac{\partial h}{\partial w_1}$. The purpose of this document is to help you learn to take derivatives of vectors, matrices, and. The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point.
Rk × K → Rn × N As A(B) = C ′ Bc.
The matrices df(y) 2 m(n;p) and dr(x) 2m(p;m) combine to the matrix product dfdrat a point.