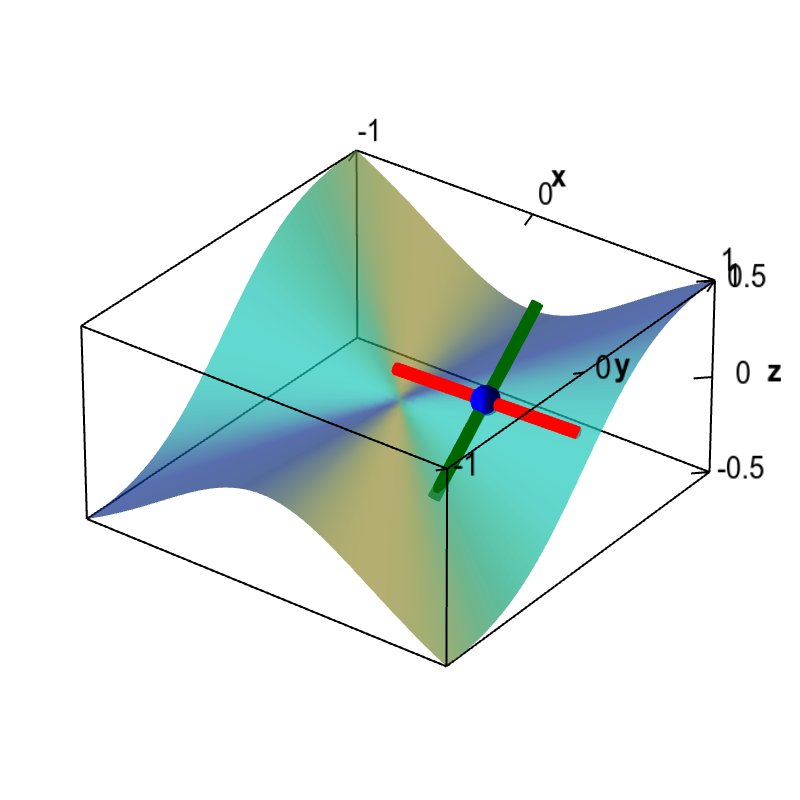
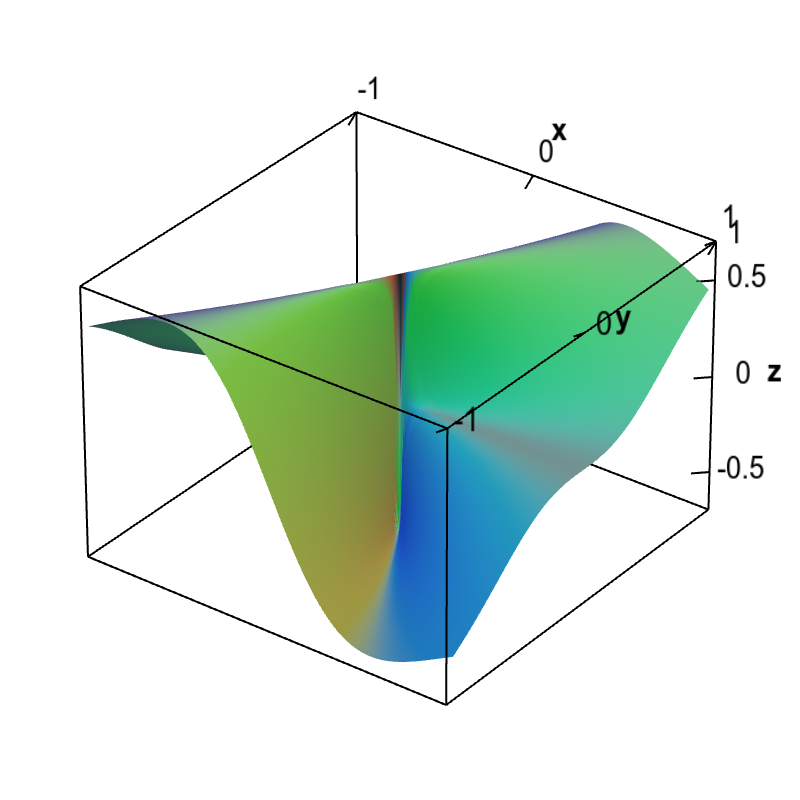
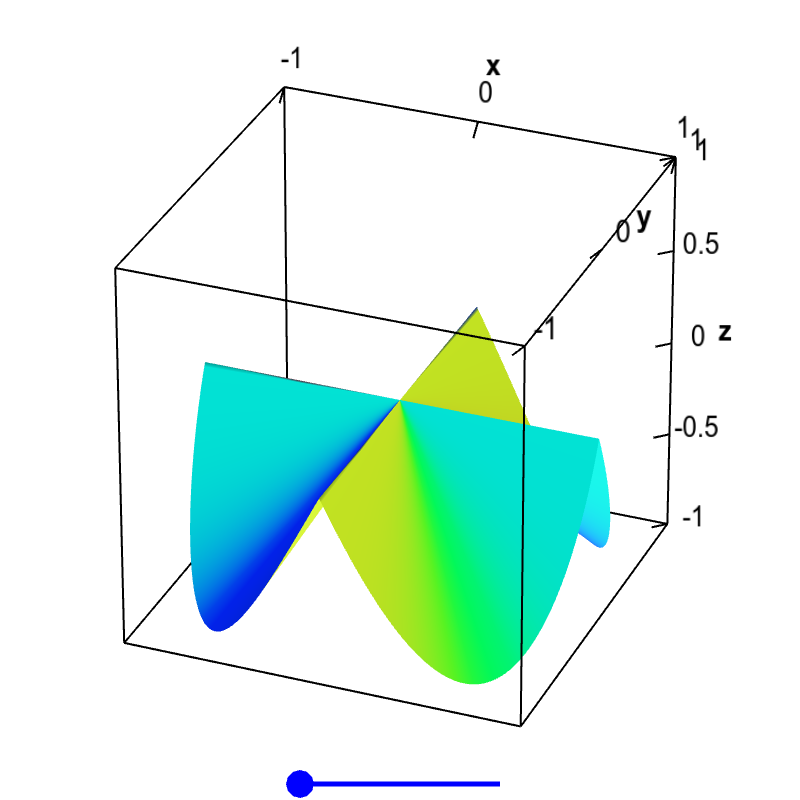Non Differentiable Functions - In the case of functions of one variable it is a function that does not have a. Differentiable functions are ones you can find a derivative (slope) for. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. If you can't find a. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function that does not have a unique tangent. How can we make sense of a delta function that isn't really a function?
Differentiable functions are ones you can find a derivative (slope) for. In the case of functions of one variable it is a function that does not have a. A function that does not have a unique tangent. How can we make sense of a delta function that isn't really a function? A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. So a point where the function is not differentiable is a point where this limit does not exist, that is,. If you can't find a.
In the case of functions of one variable it is a function that does not have a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. So a point where the function is not differentiable is a point where this limit does not exist, that is,. If you can't find a. A function that does not have a unique tangent. How can we make sense of a delta function that isn't really a function? Differentiable functions are ones you can find a derivative (slope) for.
(PDF) Newton's method for nondifferentiable functions
If you can't find a. A function that does not have a unique tangent. In the case of functions of one variable it is a function that does not have a. Differentiable functions are ones you can find a derivative (slope) for. So a point where the function is not differentiable is a point where this limit does not exist,.
2.7, Non differentiable Functions Math 231 022 JCCC Studocu
A function that does not have a unique tangent. In the case of functions of one variable it is a function that does not have a. Differentiable functions are ones you can find a derivative (slope) for. So a point where the function is not differentiable is a point where this limit does not exist, that is,. If you can't.
Differentiable function Wikiwand
So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. Differentiable functions are ones you can find a derivative (slope) for. If you can't find a. In the case.
Applet Nondifferentiable function with partial derivatives Math Insight
In the case of functions of one variable it is a function that does not have a. Differentiable functions are ones you can find a derivative (slope) for. If you can't find a. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which jumps is not differentiable.
Nondifferentiable functions must have discontinuous partial
If you can't find a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. In the case of functions of one variable it is a function that does not have a. A function that does not have a unique tangent. How can we make sense of a delta.
On Correctness of Automatic Differentiation for NonDifferentiable
Differentiable functions are ones you can find a derivative (slope) for. If you can't find a. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. A function that.
The figure shows graphs of four useful but nondifferentiable Quizlet
How can we make sense of a delta function that isn't really a function? A function that does not have a unique tangent. If you can't find a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. In the case of functions of one variable it is a.
Nondifferentiable functions must have discontinuous partial
A function that does not have a unique tangent. How can we make sense of a delta function that isn't really a function? If you can't find a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. In the case of functions of one variable it is a.
(PDF) Continuous Nowhere Differentiable Functions (MS Thesis)
A function that does not have a unique tangent. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. If you can't find a. Differentiable functions are ones you can find a derivative (slope) for. How can we make sense of a delta function that isn't really a function?
(PDF) Mountain pass theorems for nondifferentiable functions and
A function that does not have a unique tangent. So a point where the function is not differentiable is a point where this limit does not exist, that is,. If you can't find a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. How can we make sense.
A Function Which Jumps Is Not Differentiable At The Jump Nor Is One Which Has A Cusp, Like |X| Has At.
A function that does not have a unique tangent. How can we make sense of a delta function that isn't really a function? Differentiable functions are ones you can find a derivative (slope) for. In the case of functions of one variable it is a function that does not have a.
If You Can't Find A.
So a point where the function is not differentiable is a point where this limit does not exist, that is,.