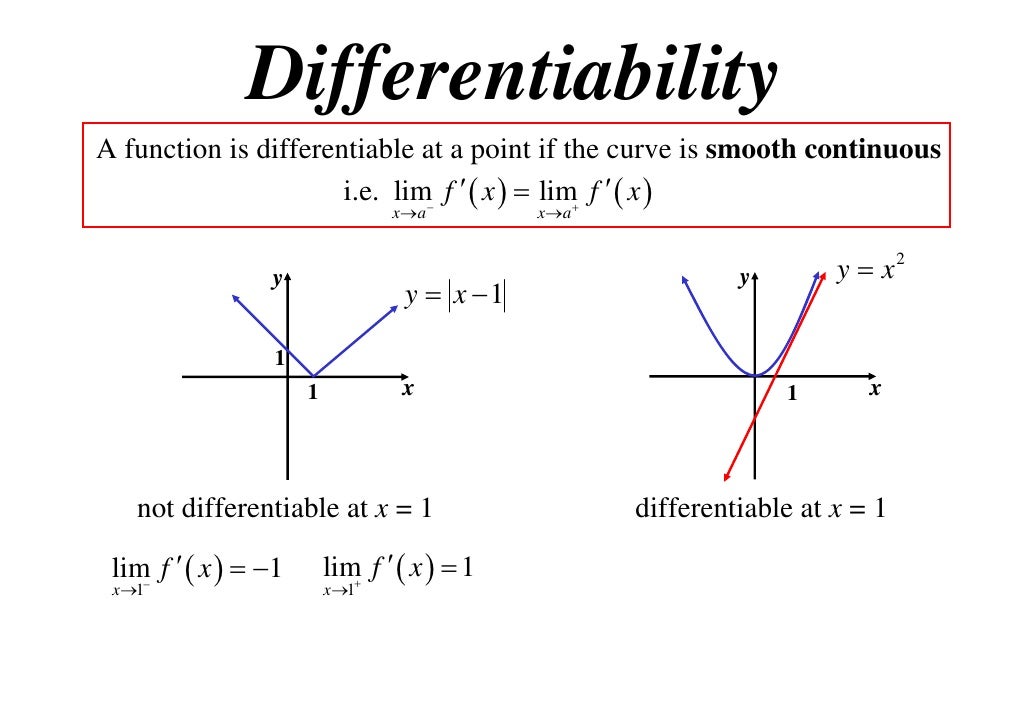
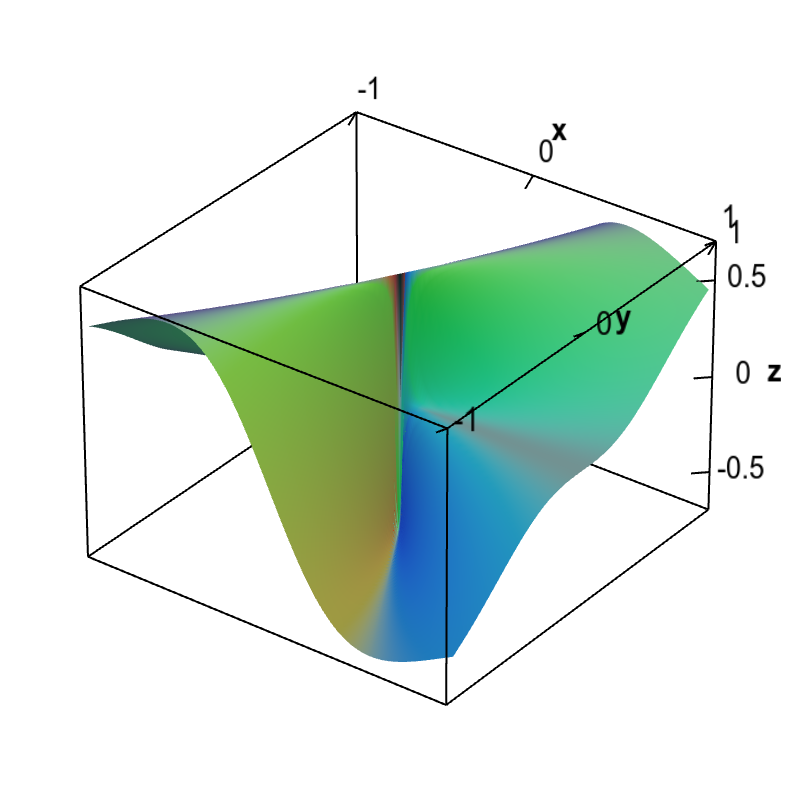
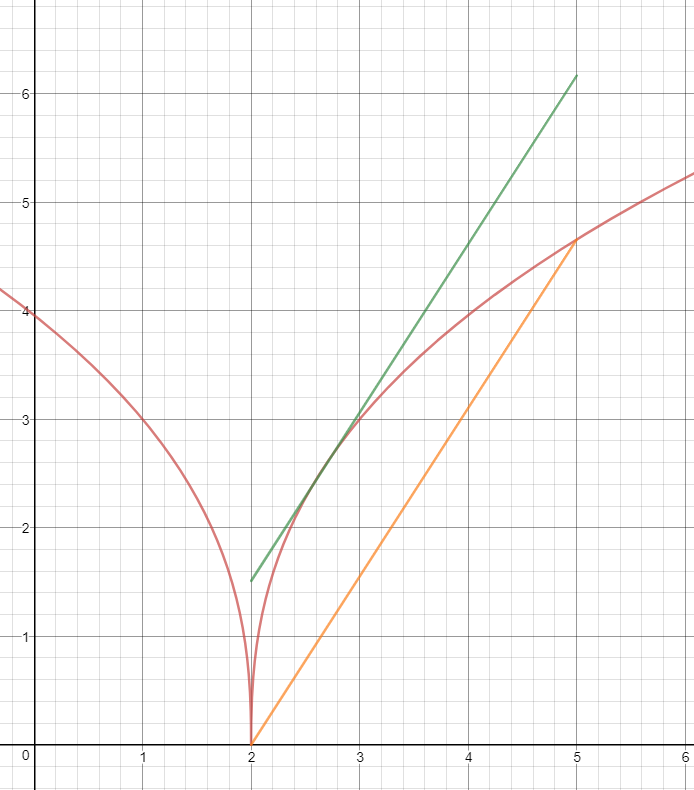
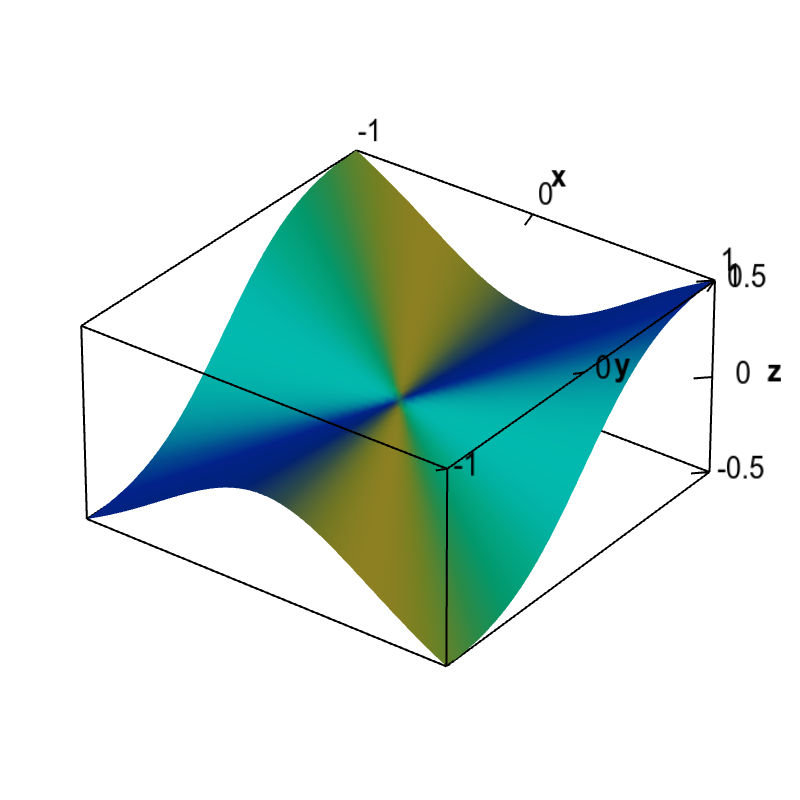Not Differentiable - A function f is not differentiable if (1) f is not continuous (2) left and right derivatives are different (3) the graph has a vertical tangent (4) the increment quotient oscillates. Courses on khan academy are always 100% free. So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is discontinuous, or where there. The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has undefined slope, hence undefined derivative). Start practicing—and saving your progress—now:
The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. Courses on khan academy are always 100% free. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has undefined slope, hence undefined derivative). So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is discontinuous, or where there. Start practicing—and saving your progress—now: A function f is not differentiable if (1) f is not continuous (2) left and right derivatives are different (3) the graph has a vertical tangent (4) the increment quotient oscillates.
We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has undefined slope, hence undefined derivative). A function f is not differentiable if (1) f is not continuous (2) left and right derivatives are different (3) the graph has a vertical tangent (4) the increment quotient oscillates. The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is discontinuous, or where there. Courses on khan academy are always 100% free. Start practicing—and saving your progress—now:
Differentiable vs. Continuous Functions Understanding the Distinctions
We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has undefined slope, hence undefined derivative). The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. Courses on khan academy are always 100%.
calculus On Differentiable Functions (Khan Academy) Mathematics
The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. Start practicing—and saving your progress—now: We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has undefined slope, hence undefined derivative). So a.
Can Something Be Differentiable but Not Continuous Quant RL
Courses on khan academy are always 100% free. The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is.
Nondifferentiable functions must have discontinuous partial
So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is discontinuous, or where there. Courses on khan academy are always 100% free. Start practicing—and saving your progress—now: The function jumps at x x, (is not continuous) like what.
Differentiable Function Meaning, Formulas and Examples Outlier
Start practicing—and saving your progress—now: The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. A function f is not differentiable if (1) f is not continuous (2) left and right derivatives are different (3) the graph has a vertical tangent (4) the increment quotient oscillates. Courses on khan academy.
When Is a Function Continuous but Not Differentiable Quant RL
So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is discontinuous, or where there. The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. Courses on khan academy.
Differentiable Function CBSE Library
The function jumps at x x, (is not continuous) like what happens at a step on a flight of stairs. So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is discontinuous, or where there. A function f is.
Why is the function not differentiable? Socratic
Courses on khan academy are always 100% free. Start practicing—and saving your progress—now: A function f is not differentiable if (1) f is not continuous (2) left and right derivatives are different (3) the graph has a vertical tangent (4) the increment quotient oscillates. So a point where the function is not differentiable is a point where this limit does.
Nondifferentiable functions must have discontinuous partial
Start practicing—and saving your progress—now: We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has undefined slope, hence undefined derivative). Courses on khan academy are always 100% free. A function f is not differentiable if (1) f is not continuous (2) left.
calculus Show f is not differentiable at x=0 Mathematics Stack Exchange
So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is discontinuous, or where there. Courses on khan academy are always 100% free. A function f is not differentiable if (1) f is not continuous (2) left and right.
We Can Say That F Is Not Differentiable For Any Value Of X Where A Tangent Cannot 'Exist' Or The Tangent Exists But Is Vertical (Vertical Line Has Undefined Slope, Hence Undefined Derivative).
Start practicing—and saving your progress—now: Courses on khan academy are always 100% free. A function f is not differentiable if (1) f is not continuous (2) left and right derivatives are different (3) the graph has a vertical tangent (4) the increment quotient oscillates. So a point where the function is not differentiable is a point where this limit does not exist, that is, is either infinite (case of a vertical tangent), where the function is discontinuous, or where there.