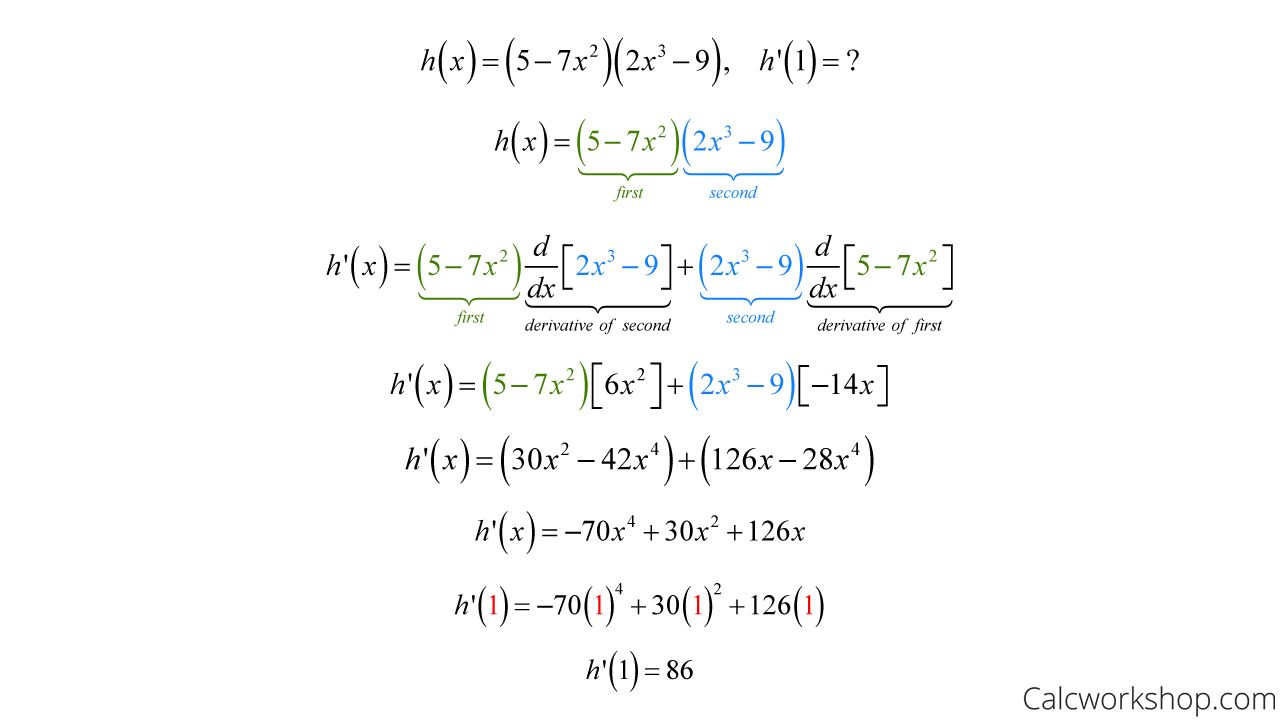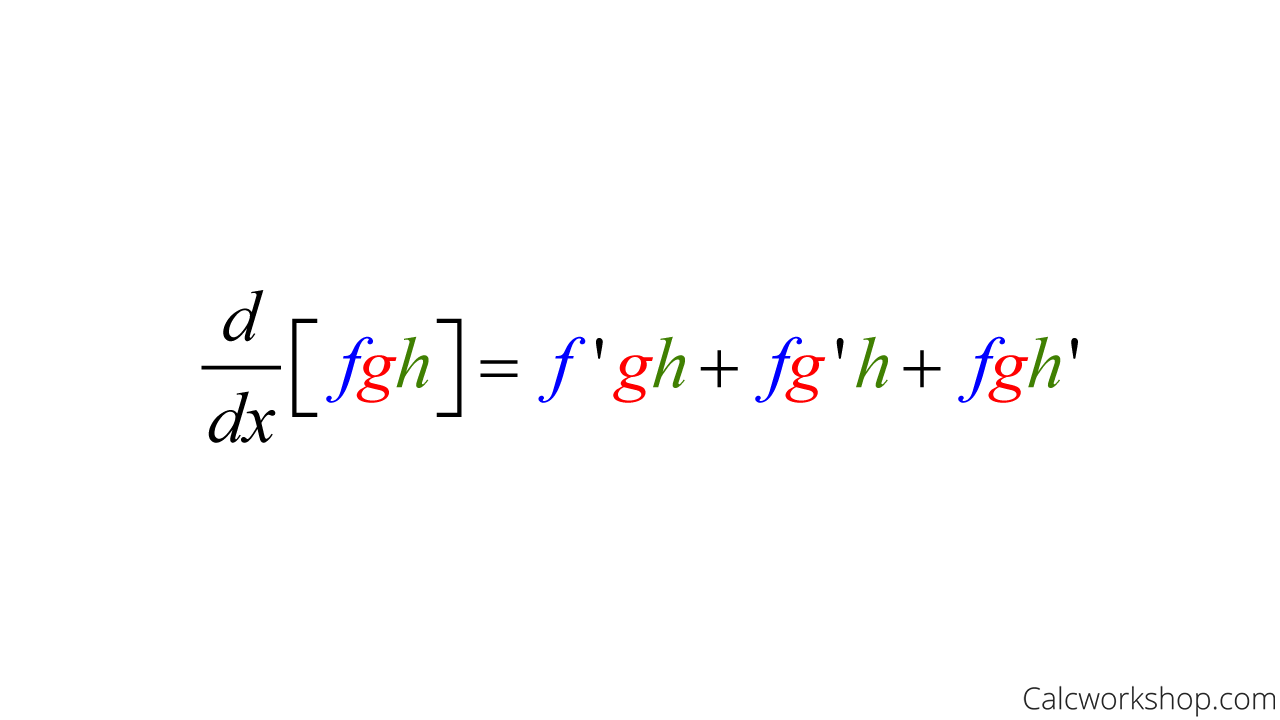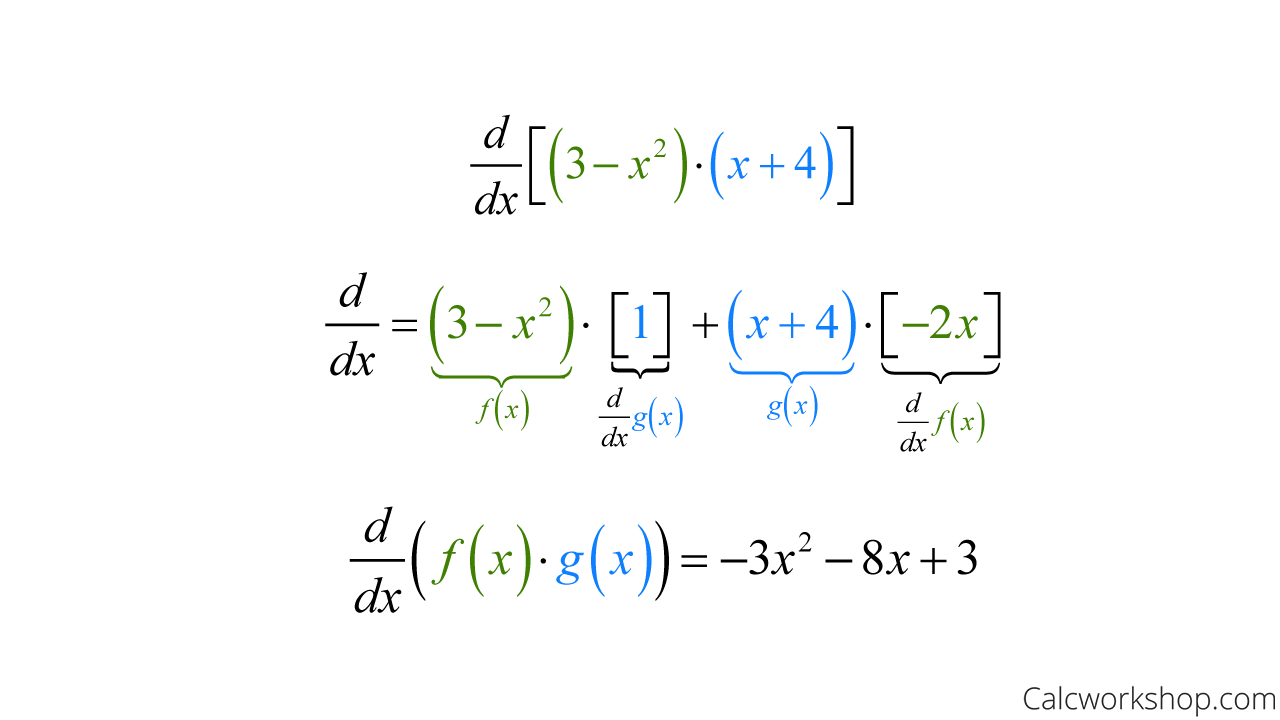Product Rule Differentiation Proof - \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. How i do i prove the product rule for derivatives? All we need to do is use the definition of the derivative alongside a simple algebraic trick. Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. The product rule is a common rule for the differentiating problems where one function is multiplied by another function. The derivative exist) then the product is. If the two functions \ (f\left ( x \right)\) and \ (g\left ( x \right)\) are differentiable (i.e. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more.
\({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. The product rule is a common rule for the differentiating problems where one function is multiplied by another function. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. The derivative exist) then the product is. If the two functions \ (f\left ( x \right)\) and \ (g\left ( x \right)\) are differentiable (i.e. How i do i prove the product rule for derivatives? Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. All we need to do is use the definition of the derivative alongside a simple algebraic trick.
The derivative exist) then the product is. Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. The product rule is a common rule for the differentiating problems where one function is multiplied by another function. \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. All we need to do is use the definition of the derivative alongside a simple algebraic trick. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. How i do i prove the product rule for derivatives? If the two functions \ (f\left ( x \right)\) and \ (g\left ( x \right)\) are differentiable (i.e.
Product Rule For Calculus (w/ StepbyStep Examples!)
The derivative exist) then the product is. All we need to do is use the definition of the derivative alongside a simple algebraic trick. Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. In calculus, the product rule (or leibniz rule[1] or.
When do I use the chain rule and when do I use the product rule in
The derivative exist) then the product is. The product rule is a common rule for the differentiating problems where one function is multiplied by another function. How i do i prove the product rule for derivatives? All we need to do is use the definition of the derivative alongside a simple algebraic trick. If the two functions \ (f\left (.
Differentiation, Product rule Teaching Resources
In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. All we need to do is use the definition of the derivative alongside a simple algebraic trick. Product rule in calculus is a method to find the derivative or differentiation of a function given.
Proof Differentiation PDF
How i do i prove the product rule for derivatives? \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. If the two functions.
How to differentiate a product of two functions Basic Algebra
All we need to do is use the definition of the derivative alongside a simple algebraic trick. \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. The derivative exist) then the product is. If the two functions \ (f\left ( x \right)\) and \ (g\left ( x \right)\) are.
Product rule differentiation Learn statement, derivation,formula
How i do i prove the product rule for derivatives? All we need to do is use the definition of the derivative alongside a simple algebraic trick. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. Product rule in calculus is a method.
Product Rule For Calculus (w/ StepbyStep Examples!)
Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. The derivative exist) then the product is. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more..
Product Rule For Calculus (w/ StepbyStep Examples!)
In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. If the two functions \ (f\left ( x \right)\) and \ (g\left ( x \right)\) are differentiable (i.e. How i do i prove the product rule for derivatives? \({\left( {f\,g} \right)^\prime } = f'\,g.
Proof of Product Rule of Differentiation
The product rule is a common rule for the differentiating problems where one function is multiplied by another function. All we need to do is use the definition of the derivative alongside a simple algebraic trick. \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. The derivative exist) then.
Chain Rule Vs Product Rule
Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. The product rule is a common rule.
How I Do I Prove The Product Rule For Derivatives?
The product rule is a common rule for the differentiating problems where one function is multiplied by another function. \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. If the two functions \ (f\left ( x \right)\) and \ (g\left ( x \right)\) are differentiable (i.e. Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two.
In Calculus, The Product Rule (Or Leibniz Rule[1] Or Leibniz Product Rule) Is A Formula Used To Find The Derivatives Of Products Of Two Or More.
All we need to do is use the definition of the derivative alongside a simple algebraic trick. The derivative exist) then the product is.