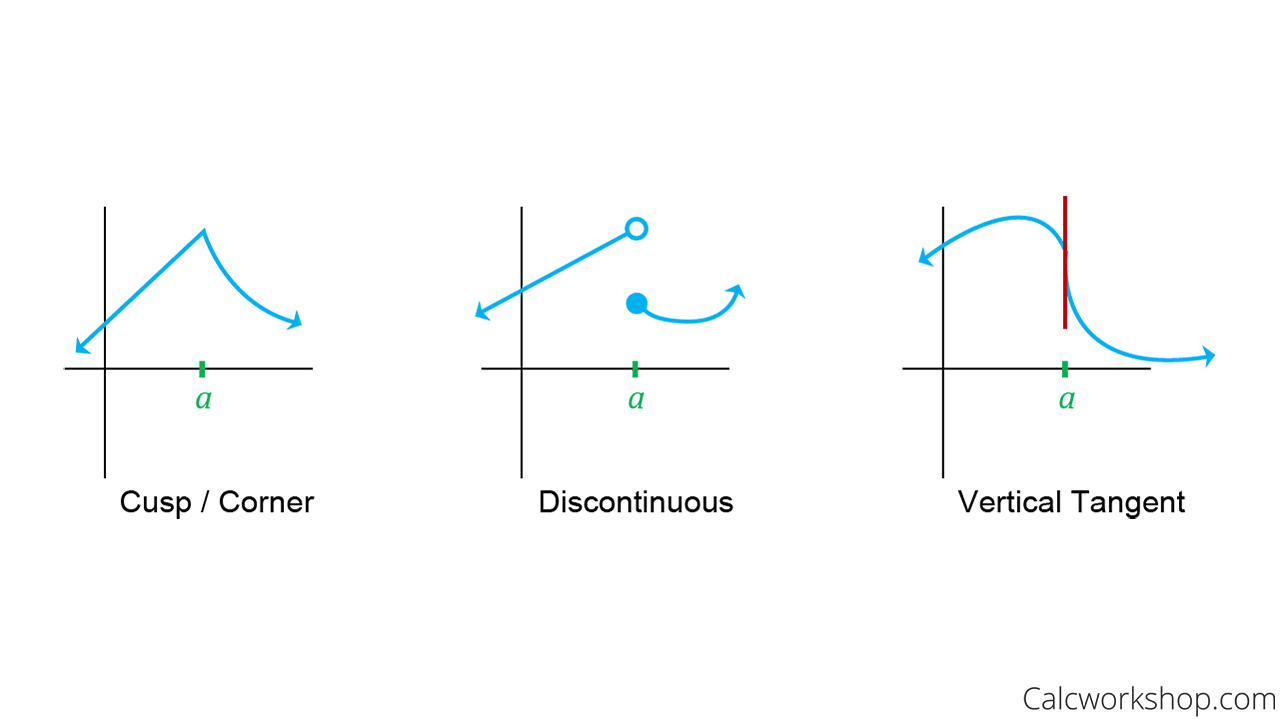
Relation Between Differentiability And Continuity - Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus.
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus.
The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by.
Worksheet 6 Continuity Differentiability PDF Function (Mathematics
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and.
PPT CONTINUITY AND DIFFERENTIABILITY PowerPoint Presentation, free
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus.
Differentiable vs. Continuous Functions Overview & Relationship
The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and.
Continuity And Differentiability Formula Sheet
Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus.
Unit 2.2 Connecting Differentiability and Continuity (Notes
The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and.
Continuity and Differentiability (Fully Explained w/ Examples!)
Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus.
real analysis Relation between continuity and differentiability
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and.
derivatives Differentiability Implies Continuity (Multivariable
Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by.
Continuity and differentiability
The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by.
Continuity and Differentiability (Fully Explained w/ Examples!)
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus.
Continuity Ensures That Functions Do Not Have Abrupt Changes Or Gaps, While Differentiability Takes This A Step Further By.
Limits, continuity, and differentiability are fundamental concepts in calculus, essential for analyzing and. The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus.