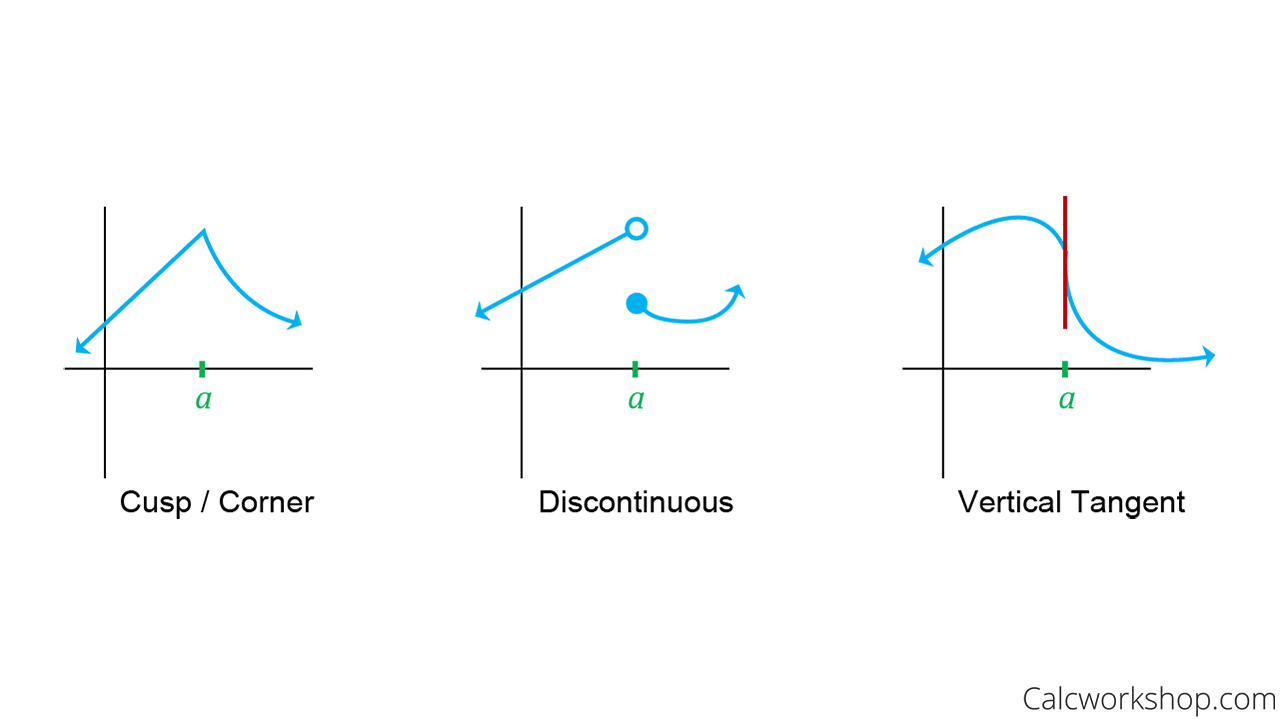
Relationship Between Differentiability And Continuity - Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability requires that a function has a defined derivative at a point,. How is differentiability different from continuity?
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. How is differentiability different from continuity? Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Differentiability requires that a function has a defined derivative at a point,.
Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability requires that a function has a defined derivative at a point,. How is differentiability different from continuity?
Using GeoGebra to verify the relationship between differentiability and
How is differentiability different from continuity? Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability requires that a function has a defined derivative at a point,. Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or.
Continuity and Differentiability (Fully Explained w/ Examples!)
Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. How is differentiability different from.
Worksheet 6 Continuity Differentiability PDF Function (Mathematics
Differentiability requires that a function has a defined derivative at a point,. Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. How is differentiability different from.
Continuity and Differentiability (Fully Explained w/ Examples!)
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Differentiability requires that a function has a defined derivative at a point,. How is differentiability different from.
3.5 Relationship Between Differentiability and Continuity, and
Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. How is differentiability different from continuity? Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or.
Differentiable vs. Continuous Functions Overview & Relationship
How is differentiability different from continuity? Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further.
Solved Determine the relationship between differentiability and
Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. How is differentiability different from continuity? Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further.
derivatives Differentiability Implies Continuity (Multivariable
How is differentiability different from continuity? Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Differentiability requires that a function has a defined derivative at a.
SOLUTION Basic calculus 11 relationship between continuity and
Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. How is differentiability different from continuity? Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability requires that a function has a defined derivative at a.
Solved Determine the relationship between differentiability and
How is differentiability different from continuity? Differentiability requires that a function has a defined derivative at a point,. Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further.
How Is Differentiability Different From Continuity?
Differentiability requires that a function has a defined derivative at a point,. Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by.