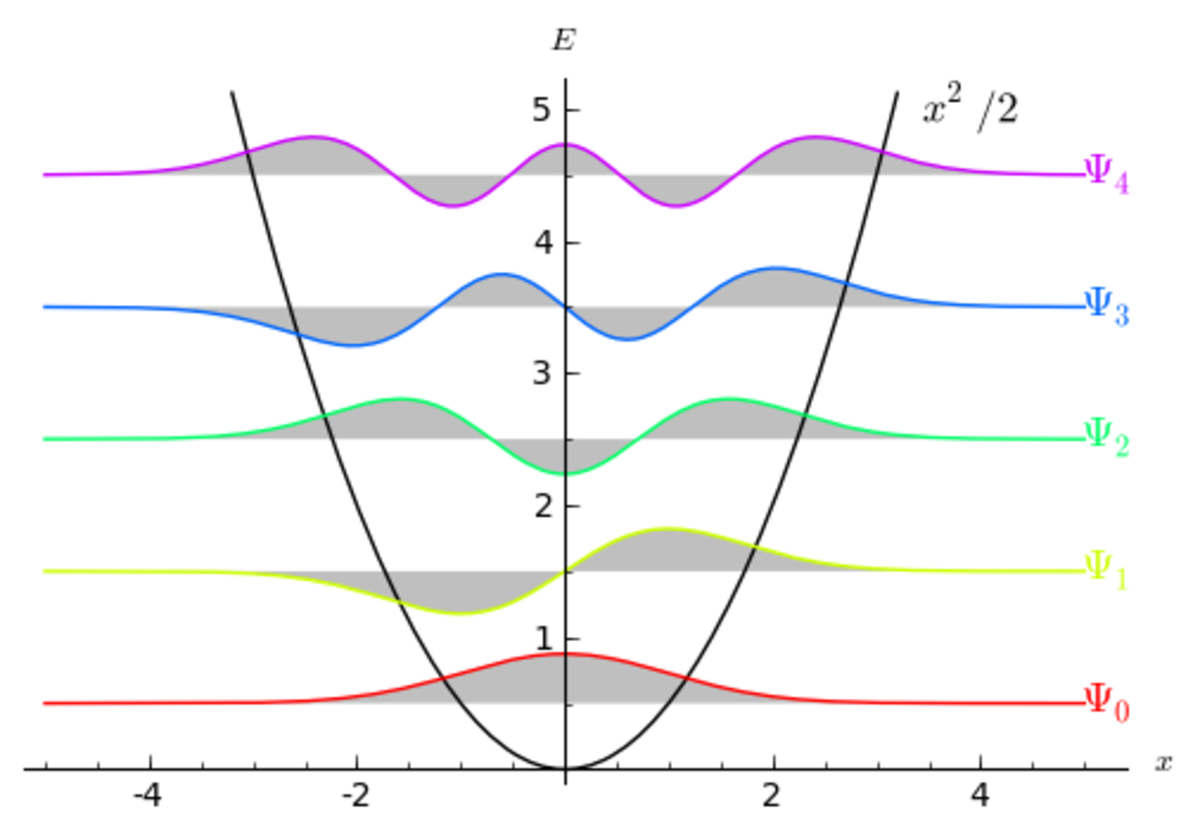
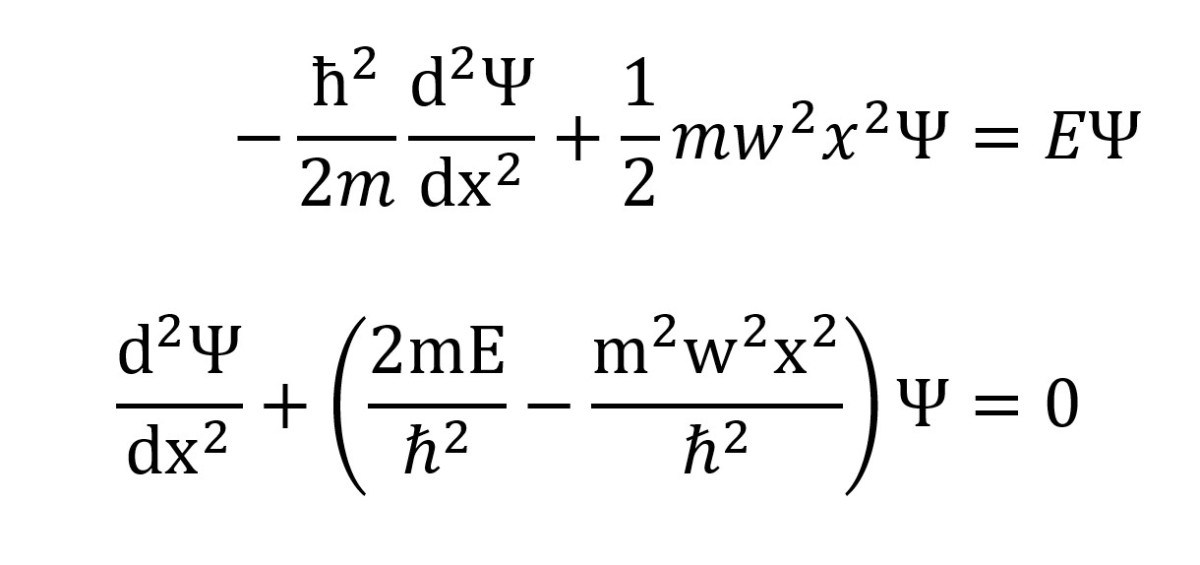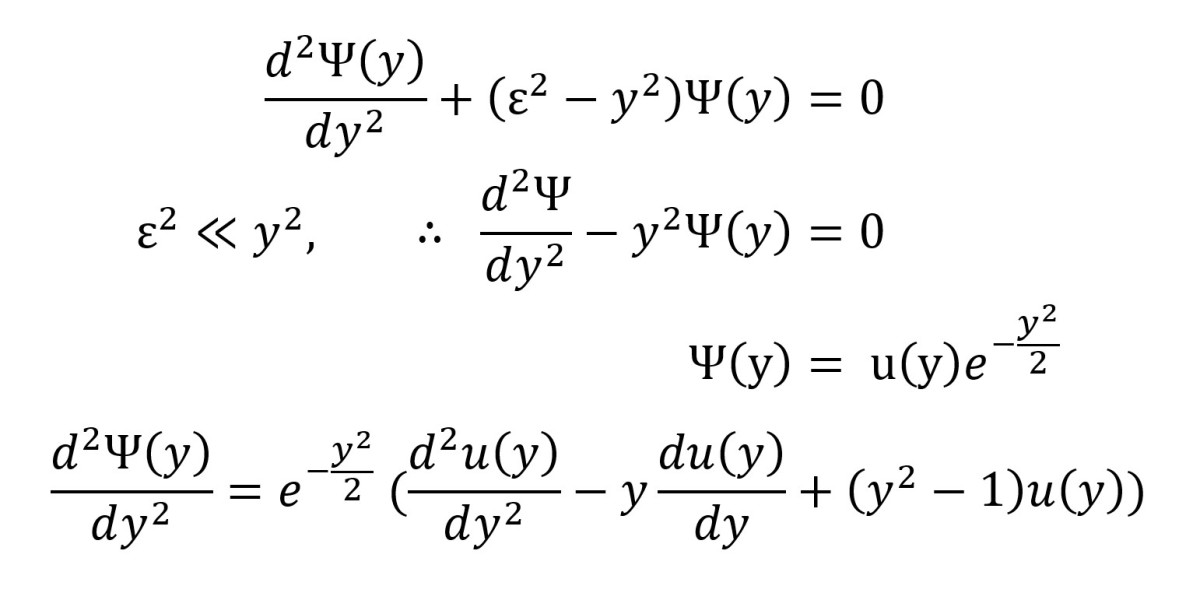Simple Harmonic Oscillator Differential Equation - The solution to our differential equation is an algebraic equation — position as a function of time (x (t)) — that is also a trigonometric equation. Simple harmonic oscillator equation (sho). How to solve harmonic oscillator differential equation: Because the spring force depends on the distance. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Displacement as a function of time we wish to solve the equation. The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a. X, the acceleration is not constant. Solving the simple harmonic oscillator 1.
$\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Displacement as a function of time we wish to solve the equation. Solving the simple harmonic oscillator 1. Because the spring force depends on the distance. X, the acceleration is not constant. The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a. How to solve harmonic oscillator differential equation: The solution to our differential equation is an algebraic equation — position as a function of time (x (t)) — that is also a trigonometric equation. Simple harmonic oscillator equation (sho).
How to solve harmonic oscillator differential equation: $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ The solution to our differential equation is an algebraic equation — position as a function of time (x (t)) — that is also a trigonometric equation. Solving the simple harmonic oscillator 1. Displacement as a function of time we wish to solve the equation. Simple harmonic oscillator equation (sho). Because the spring force depends on the distance. X, the acceleration is not constant. The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a.
SOLVED the homogenous linear differential equation d^2X/dt^2 +w^2X=0
The solution to our differential equation is an algebraic equation — position as a function of time (x (t)) — that is also a trigonometric equation. Because the spring force depends on the distance. How to solve harmonic oscillator differential equation: $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ X, the acceleration is not constant.
simple harmonic oscillator differential equation DriverLayer Search
$\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Displacement as a function of time we wish to solve the equation. Solving the simple harmonic oscillator 1. The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a. How to solve harmonic oscillator differential equation:
Solution of Schrödinger Equation for Simple Harmonic Oscillator Owlcation
How to solve harmonic oscillator differential equation: The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a. Simple harmonic oscillator equation (sho). The solution to our differential equation is an algebraic equation — position as a function of time (x (t)) — that is also a trigonometric equation. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$
simple harmonic oscillator differential equation DriverLayer Search
Simple harmonic oscillator equation (sho). The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a. Displacement as a function of time we wish to solve the equation. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ X, the acceleration is not constant.
Solution of Schrödinger Equation for Simple Harmonic Oscillator Owlcation
Simple harmonic oscillator equation (sho). X, the acceleration is not constant. Solving the simple harmonic oscillator 1. How to solve harmonic oscillator differential equation: The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a.
Solved A simple harmonic oscillator obeys the differential
How to solve harmonic oscillator differential equation: Because the spring force depends on the distance. The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a. Solving the simple harmonic oscillator 1. X, the acceleration is not constant.
Solution of Schrödinger Equation for Simple Harmonic Oscillator Owlcation
Because the spring force depends on the distance. Solving the simple harmonic oscillator 1. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Simple harmonic oscillator equation (sho). The solution to our differential equation is an algebraic equation — position as a function of time (x (t)) — that is also a trigonometric equation.
Harmonic oscillator equation poretkings
Because the spring force depends on the distance. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a. How to solve harmonic oscillator differential equation: X, the acceleration is not constant.
Harmonic oscillator equation psadojoe
Because the spring force depends on the distance. The solution to our differential equation is an algebraic equation — position as a function of time (x (t)) — that is also a trigonometric equation. X, the acceleration is not constant. How to solve harmonic oscillator differential equation: Solving the simple harmonic oscillator 1.
harmonicoscillator · GitHub Topics · GitHub
The simple harmonic oscillator, a nonrelativistic particle in a potential \(\frac{1}{2}kx^2\), is an excellent model for a. Solving the simple harmonic oscillator 1. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ How to solve harmonic oscillator differential equation: Because the spring force depends on the distance.
The Simple Harmonic Oscillator, A Nonrelativistic Particle In A Potential \(\Frac{1}{2}Kx^2\), Is An Excellent Model For A.
Solving the simple harmonic oscillator 1. The solution to our differential equation is an algebraic equation — position as a function of time (x (t)) — that is also a trigonometric equation. How to solve harmonic oscillator differential equation: X, the acceleration is not constant.
$\Dfrac{D^2X}{Dt^2} + \Dfrac{Kx}{M} = 0$
Because the spring force depends on the distance. Displacement as a function of time we wish to solve the equation. Simple harmonic oscillator equation (sho).