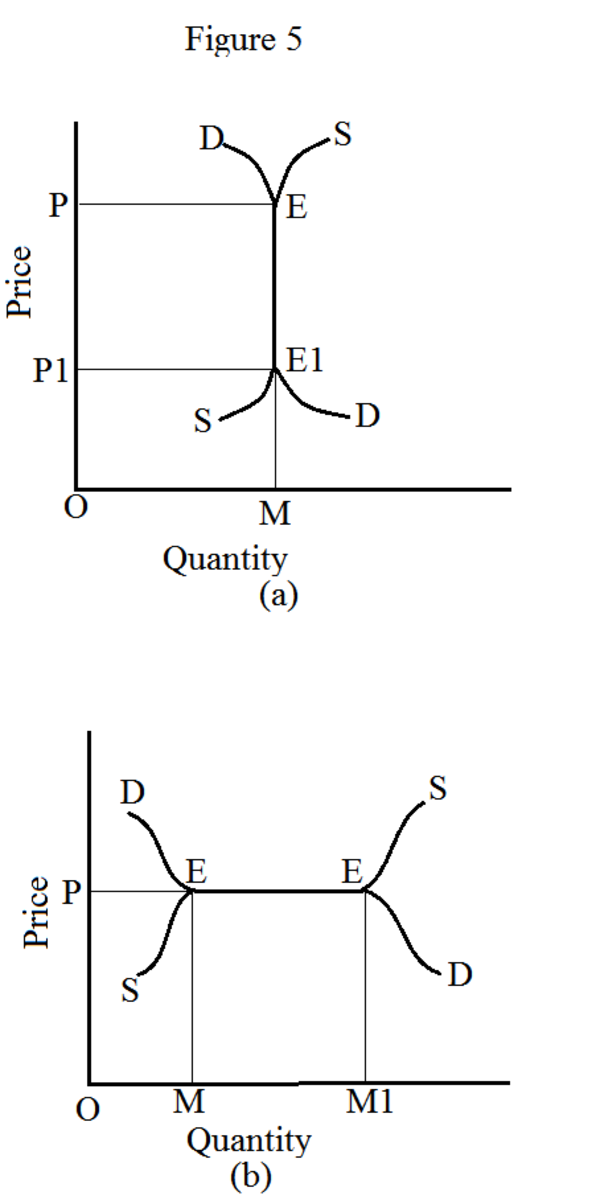
Stable Or Unstable Equilibrium Differential Equations - From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. The first one is inconclusive, it could be stable or. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that.
Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. The first one is inconclusive, it could be stable or. From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that.
The first one is inconclusive, it could be stable or. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions.
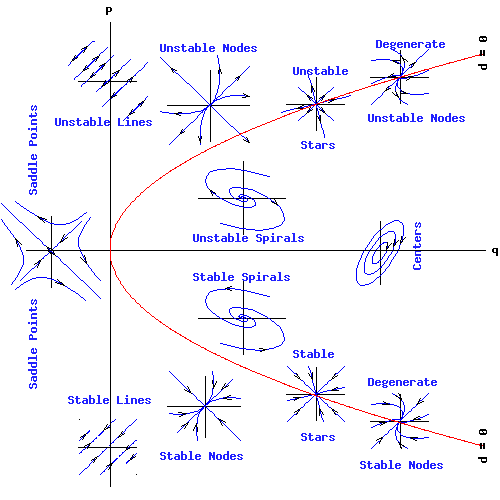
ordinary differential equations Stable/unstable equilibrium points
Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y.
classical mechanics Situation of Stable, Neutral and Unstable
From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. Recall.
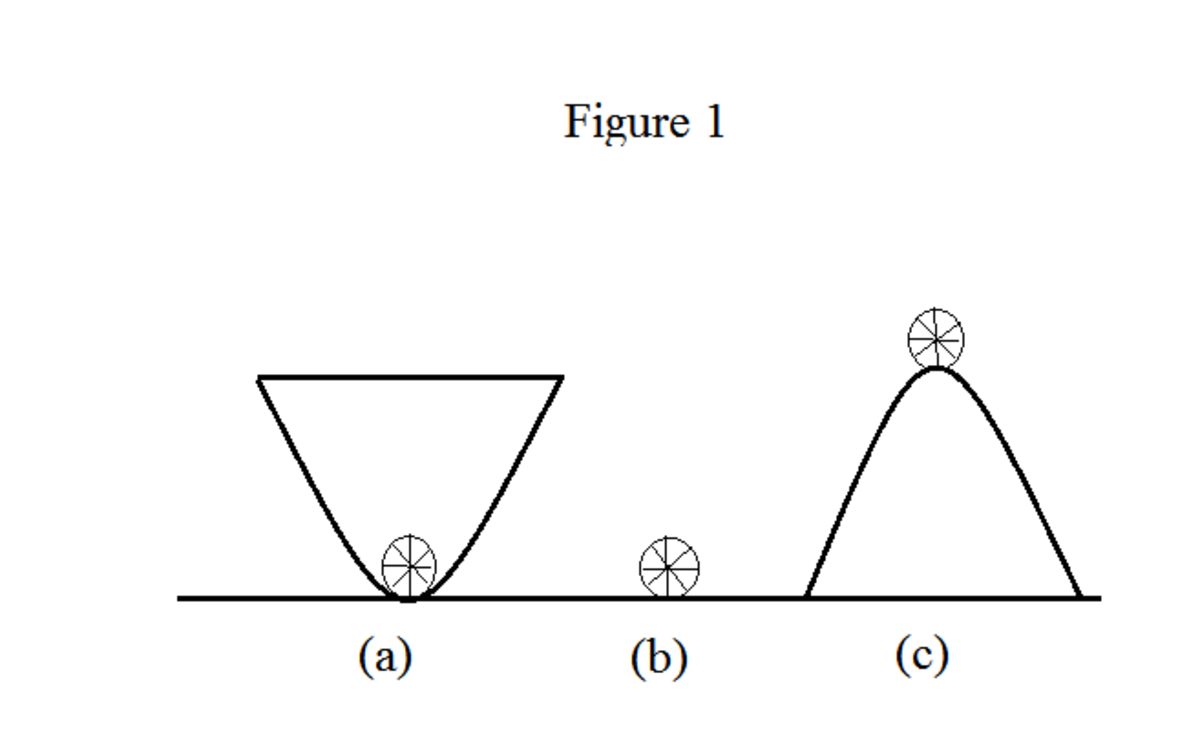
Stable and Unstable Equilibrium Owlcation
Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y.
Stable and Unstable Equilibrium Owlcation
Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. Identifying stable and unstable equilibria.
Stable and Unstable Equilibrium Owlcation
From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial.
[Solved] Determine all equilibrium solutions and classify
From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. The first one is inconclusive,.
Stable and Unstable Equilibrium Owlcation
From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. The.
Egwald Mathematics Linear Algebra Systems of Linear Differential
Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. The first one is inconclusive, it could be stable or. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. From the equation y′ = 4y2(4.
What is the difference between stable equilibrium and unstable
The first one is inconclusive, it could be stable or. From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. Recall that an equilibrium solution is any constant (horizontal).
SOLUTION Differential equilibrium equations and strain disp equations
The first one is inconclusive, it could be stable or. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. Identifying stable and unstable equilibria of a differential equation by graphically solving the equation for nearby initial conditions. Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. From the equation y′ = 4y2(4.
Identifying Stable And Unstable Equilibria Of A Differential Equation By Graphically Solving The Equation For Nearby Initial Conditions.
Autonomous differential equations sometimes have constant solutions that we call equilibrium solutions. Recall that an equilibrium solution is any constant (horizontal) function y(t) = c that. From the equation y′ = 4y2(4 −y2) y ′ = 4 y 2 (4 − y 2), the fixed points are 0 0, −2 − 2, and 2 2. The first one is inconclusive, it could be stable or.


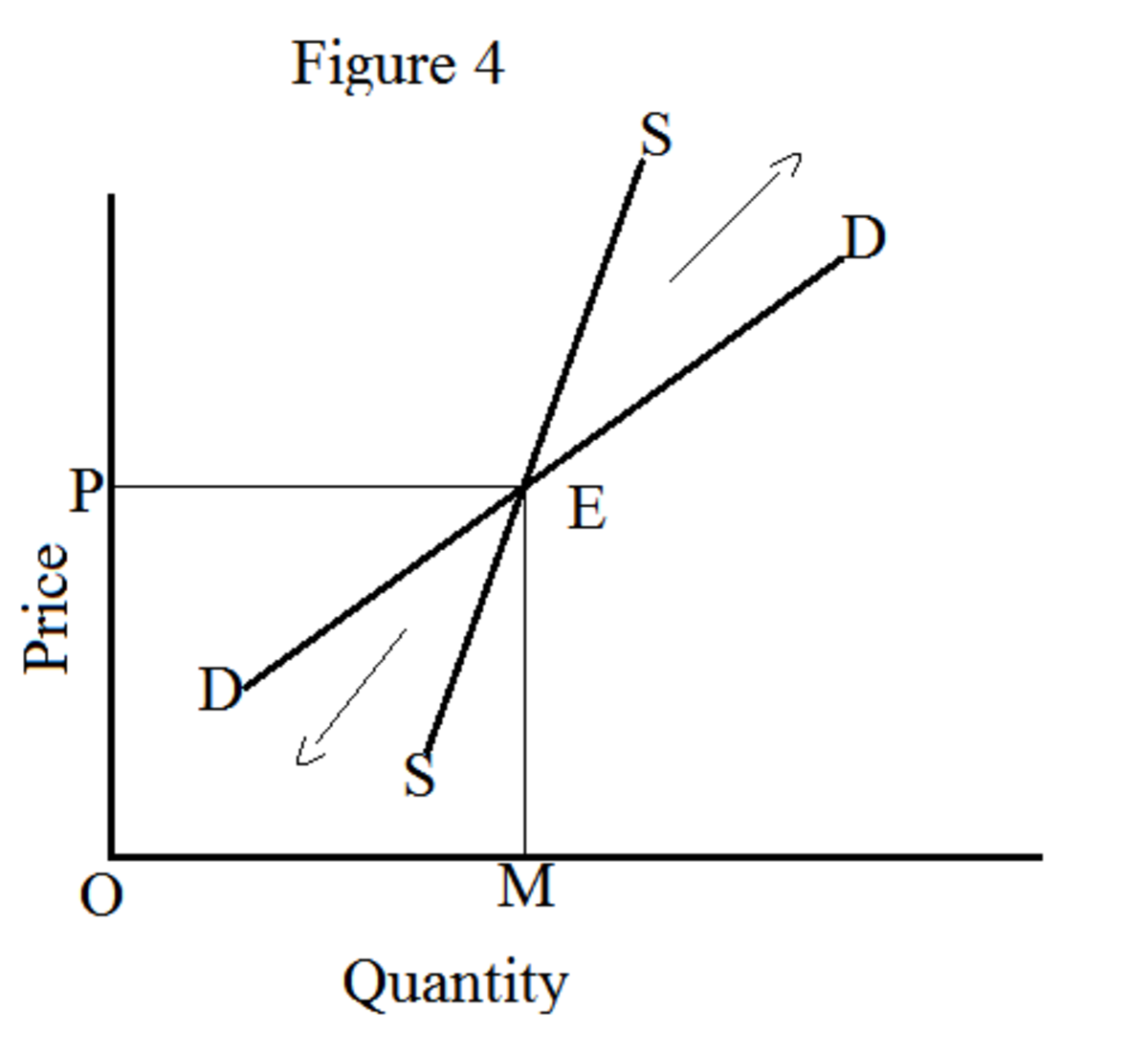
![[Solved] Determine all equilibrium solutions and classify](https://media.cheggcdn.com/media/65c/65c8f76d-93f4-4215-820e-0080eaf1203a/phphhIO7U)