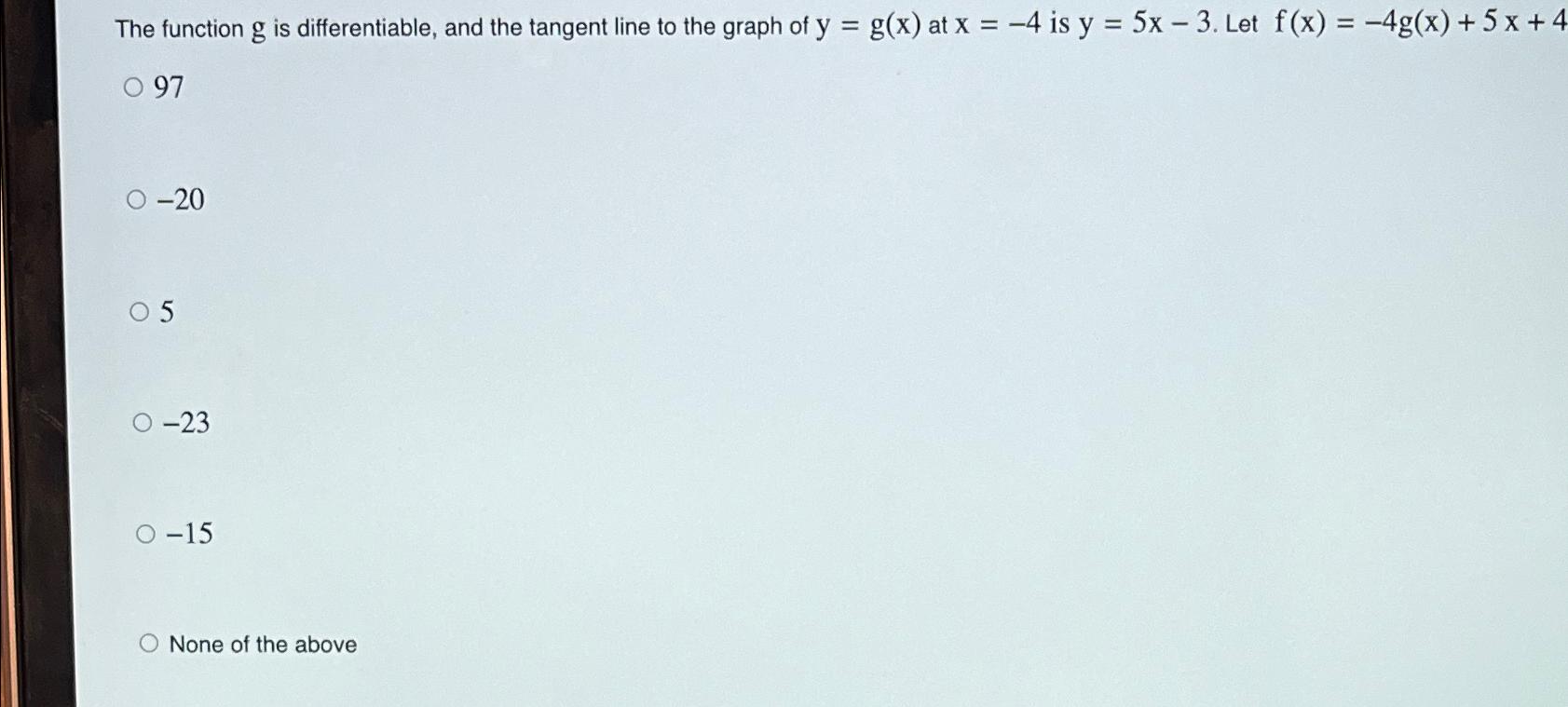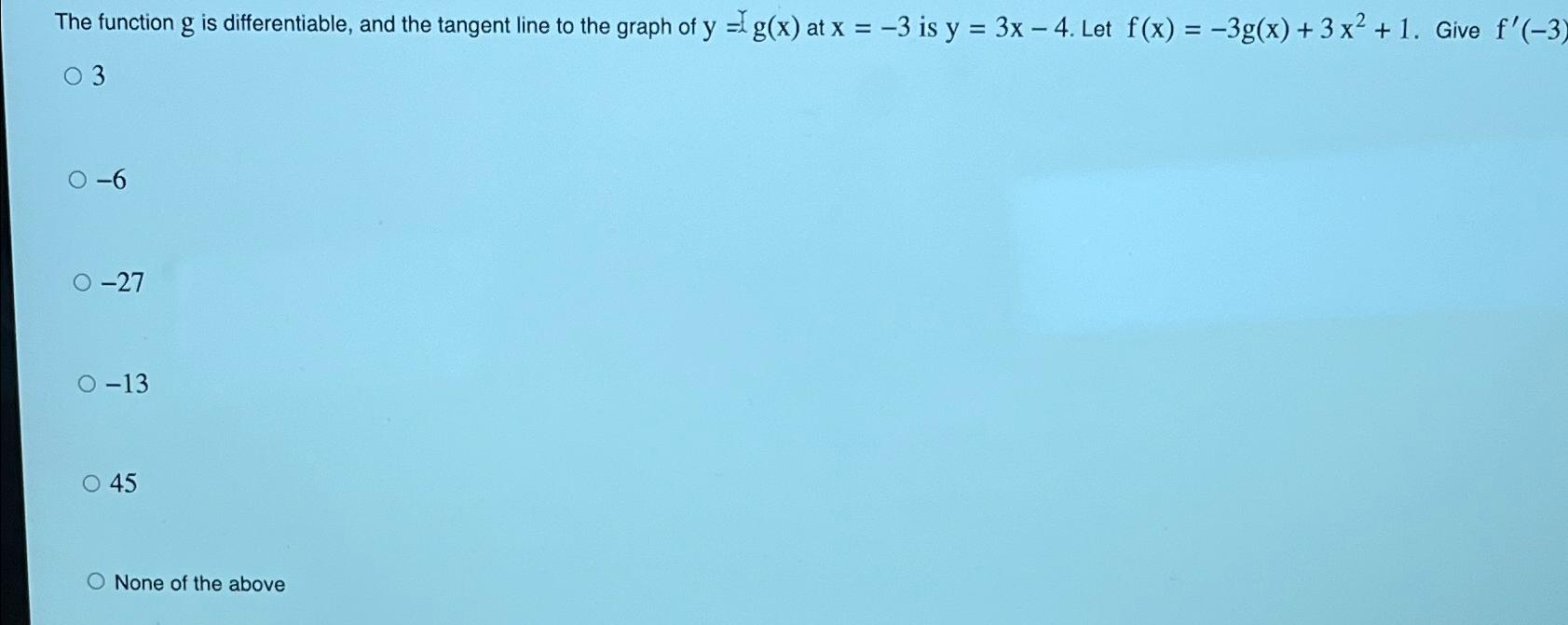The Thet Tangent Function Differentiable - In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine the slope of a line. In r2 r 2, we can interpret this definition as saying that a function f f is differentiable at a vector a⇀ a ⇀ if there is a plane l(x⇀) l (x ⇀) at that. How do we find the equation of the plane tangent to a locally linear function at a point? What is the differential of a multivariable. 2) rather than tangent lines,. In this section we extend these ideas to functions z = f(x,y) of two variables. But here we will find tangent planes (fig.
2) rather than tangent lines,. What is the differential of a multivariable. In this section we extend these ideas to functions z = f(x,y) of two variables. How do we find the equation of the plane tangent to a locally linear function at a point? In r2 r 2, we can interpret this definition as saying that a function f f is differentiable at a vector a⇀ a ⇀ if there is a plane l(x⇀) l (x ⇀) at that. In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine the slope of a line. But here we will find tangent planes (fig.
What is the differential of a multivariable. 2) rather than tangent lines,. In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine the slope of a line. How do we find the equation of the plane tangent to a locally linear function at a point? In this section we extend these ideas to functions z = f(x,y) of two variables. In r2 r 2, we can interpret this definition as saying that a function f f is differentiable at a vector a⇀ a ⇀ if there is a plane l(x⇀) l (x ⇀) at that. But here we will find tangent planes (fig.
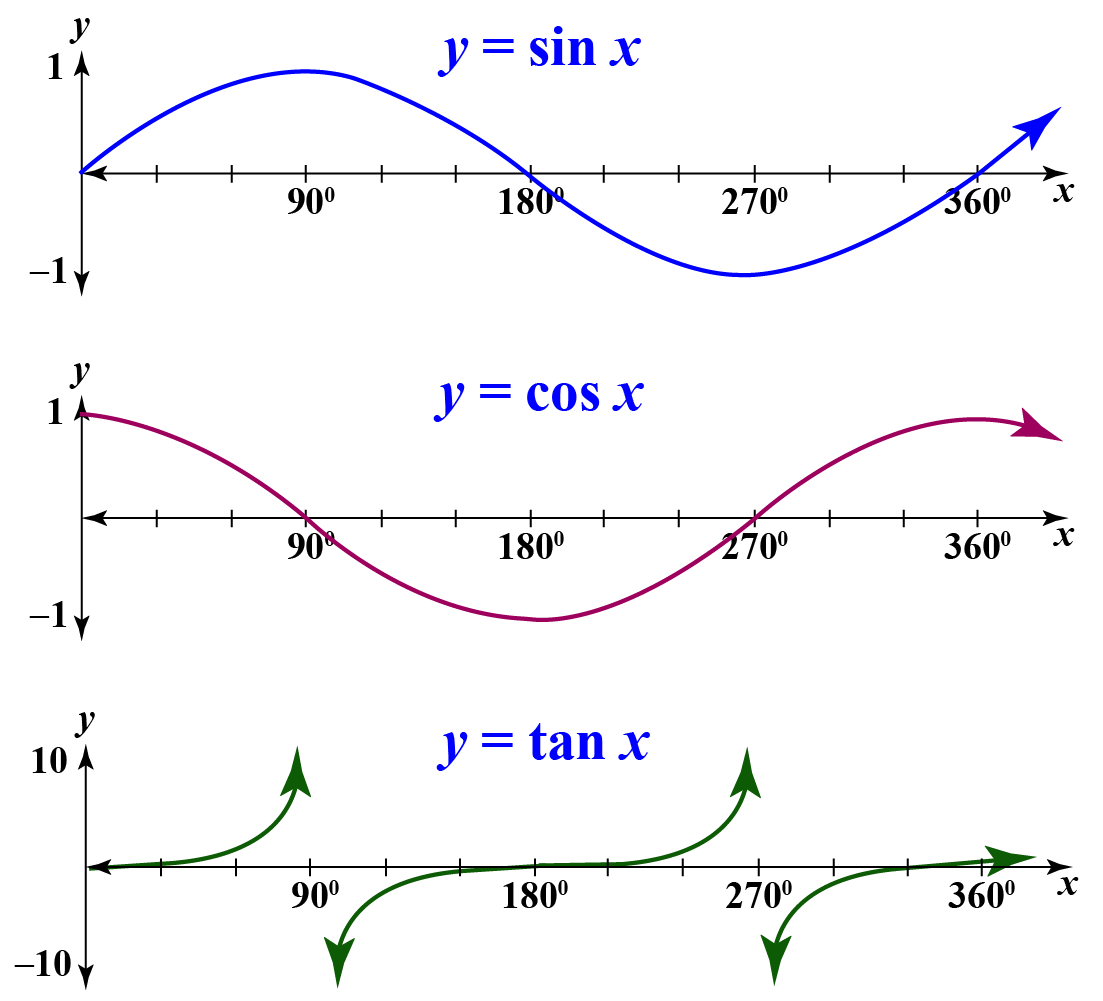
Tangent Function Tan Graph Solved Examples Cuemath
How do we find the equation of the plane tangent to a locally linear function at a point? What is the differential of a multivariable. 2) rather than tangent lines,. In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine the slope of a line. But here we.
The Tangent Function Formula + Graph
How do we find the equation of the plane tangent to a locally linear function at a point? In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine the slope of a line. But here we will find tangent planes (fig. 2) rather than tangent lines,. What is.
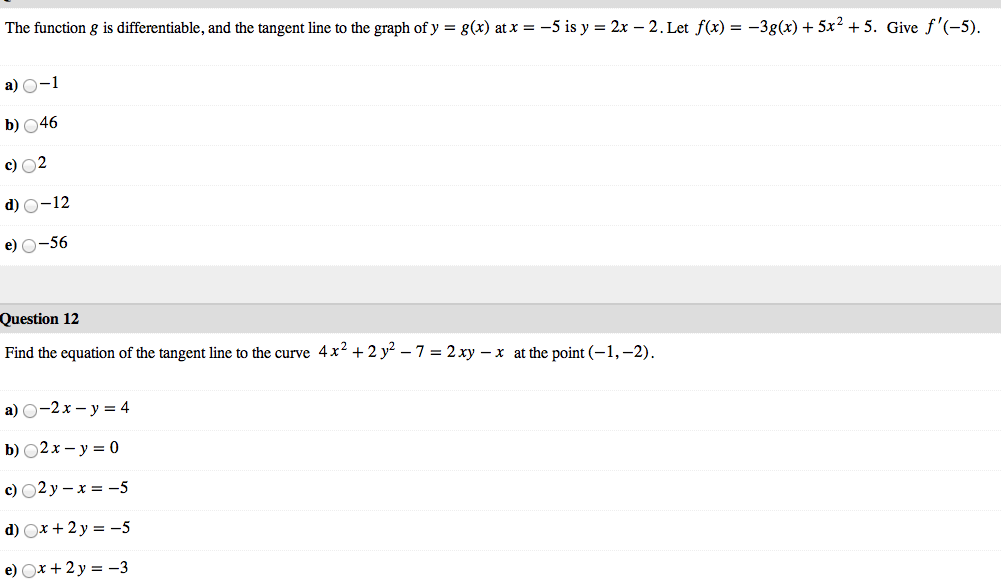
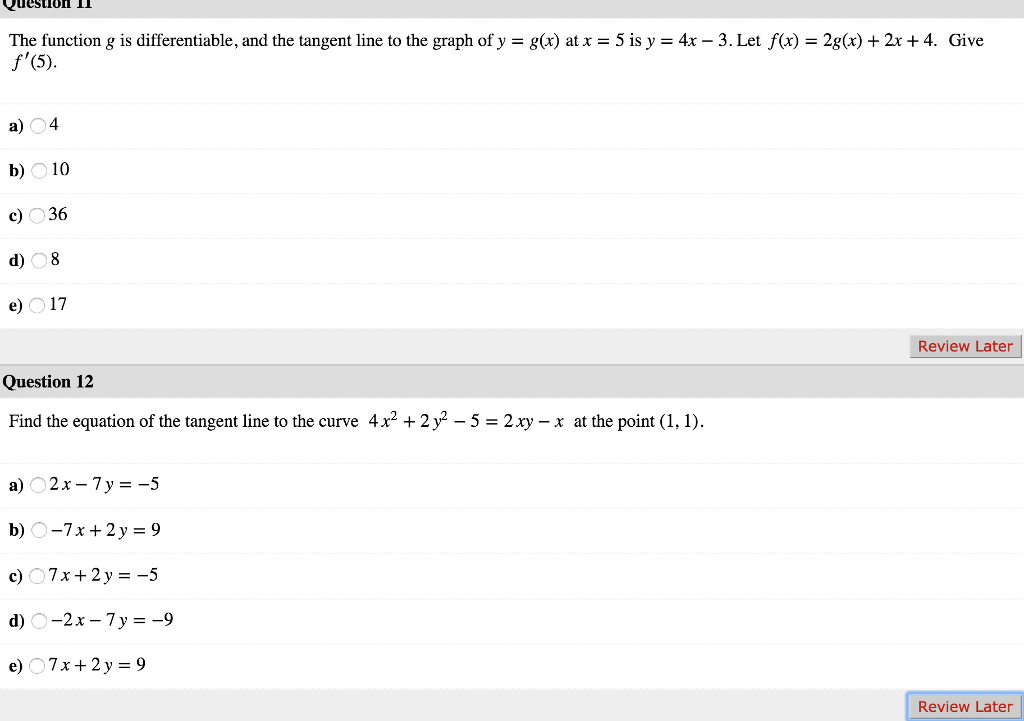
Solved The function g is differentiable, and the tangent
But here we will find tangent planes (fig. In r2 r 2, we can interpret this definition as saying that a function f f is differentiable at a vector a⇀ a ⇀ if there is a plane l(x⇀) l (x ⇀) at that. 2) rather than tangent lines,. In this section we extend these ideas to functions z = f(x,y).
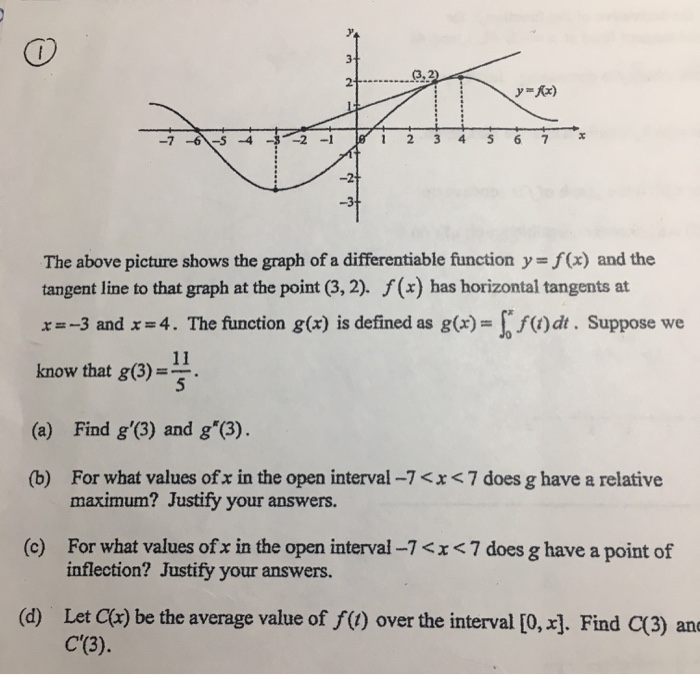
Solved The Above Picture Shows The Graph Of A Differentia...
How do we find the equation of the plane tangent to a locally linear function at a point? In r2 r 2, we can interpret this definition as saying that a function f f is differentiable at a vector a⇀ a ⇀ if there is a plane l(x⇀) l (x ⇀) at that. But here we will find tangent planes.
Solved The function g is differentiable, and the tangent
In this section we extend these ideas to functions z = f(x,y) of two variables. 2) rather than tangent lines,. In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine the slope of a line. How do we find the equation of the plane tangent to a locally.
Solved The function g is differentiable, and the tangent
But here we will find tangent planes (fig. In this section we extend these ideas to functions z = f(x,y) of two variables. How do we find the equation of the plane tangent to a locally linear function at a point? What is the differential of a multivariable. 2) rather than tangent lines,.
Differentiable function Wikiwand
In r2 r 2, we can interpret this definition as saying that a function f f is differentiable at a vector a⇀ a ⇀ if there is a plane l(x⇀) l (x ⇀) at that. In this section we extend these ideas to functions z = f(x,y) of two variables. 2) rather than tangent lines,. What is the differential of.
Solved The function g is differentiable, and the tangent
In r2 r 2, we can interpret this definition as saying that a function f f is differentiable at a vector a⇀ a ⇀ if there is a plane l(x⇀) l (x ⇀) at that. 2) rather than tangent lines,. In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a),.
Solved An equation for the line tangent to the graph of the
What is the differential of a multivariable. 2) rather than tangent lines,. How do we find the equation of the plane tangent to a locally linear function at a point? But here we will find tangent planes (fig. In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine.
Solved The function g is differentiable, and the tangent
But here we will find tangent planes (fig. In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine the slope of a line. What is the differential of a multivariable. 2) rather than tangent lines,. In r2 r 2, we can interpret this definition as saying that a.
But Here We Will Find Tangent Planes (Fig.
2) rather than tangent lines,. In chapter 2, working with a function of a single variable, f(x), we developed the definition of the derivative, f0(a), to determine the slope of a line. How do we find the equation of the plane tangent to a locally linear function at a point? In r2 r 2, we can interpret this definition as saying that a function f f is differentiable at a vector a⇀ a ⇀ if there is a plane l(x⇀) l (x ⇀) at that.
In This Section We Extend These Ideas To Functions Z = F(X,Y) Of Two Variables.
What is the differential of a multivariable.