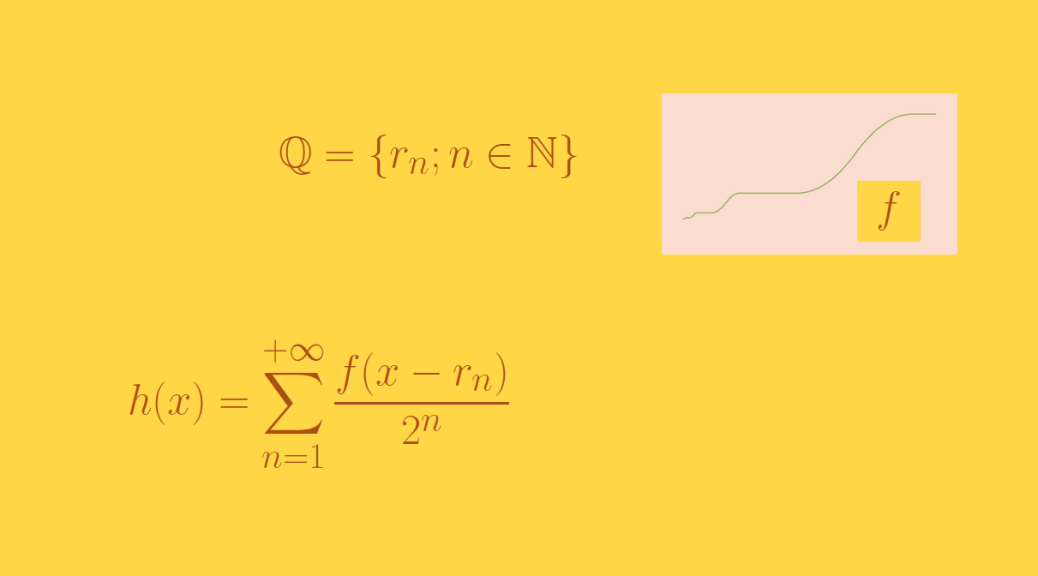Totally Differentiable - Total differentials can be generalized. Let \(dx\), \(dy\) and \(dz\) represent changes. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). We can use this to approximate error propagation;. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. The total differential gives an approximation of the change in z given small changes in x and y. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f.
Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Total differentials can be generalized. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. Let \(dx\), \(dy\) and \(dz\) represent changes. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. We can use this to approximate error propagation;. The total differential gives an approximation of the change in z given small changes in x and y.
Let \(dx\), \(dy\) and \(dz\) represent changes. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Total differentials can be generalized. We can use this to approximate error propagation;. The total differential gives an approximation of the change in z given small changes in x and y. Let \(w=f(x,y,z)\) be continuous on an open set \(s\).
Solved A5. Prove that if f D → R2 is totally
Total differentials can be generalized. The total differential gives an approximation of the change in z given small changes in x and y. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. We can use this to approximate error propagation;. Let \(w=f(x,y,z)\) be continuous on an open set.
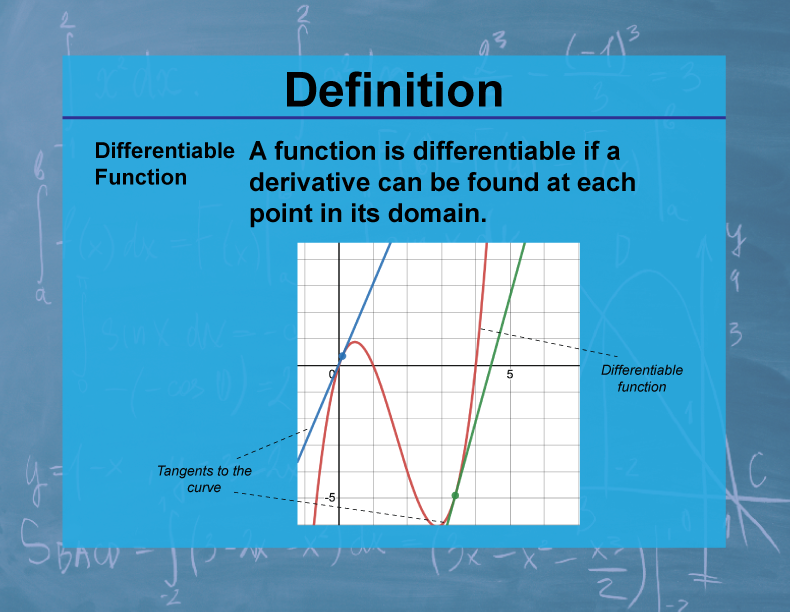
DefinitionCalculus TopicsDifferentiable Function Media4Math
Let \(dx\), \(dy\) and \(dz\) represent changes. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. The total differential gives an approximation of the change in z given small changes in x and y. Total differentials can be generalized..
Differentiable function Wikiwand
For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. Total differentials can be generalized. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Let \(dx\), \(dy\) and.
Continuous but Nowhere Differentiable Math Fun Facts
We can use this to approximate error propagation;. Total differentials can be generalized. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. The former part of δ x is called the (total) differential or the exact differential of.
Differentiable Font download free
The total differential gives an approximation of the change in z given small changes in x and y. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Total differentials can.
Differentiable vs. Continuous Functions Understanding the Distinctions
The total differential gives an approximation of the change in z given small changes in x and y. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). We can use this to approximate error propagation;. Total differentials can be generalized. Let \(dx\), \(dy\) and \(dz\) represent changes.
PPT Differentiable functions are Continuous PowerPoint Presentation
The total differential gives an approximation of the change in z given small changes in x and y. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). We can use this to approximate error propagation;. Let \(dx\), \(dy\) and \(dz\) represent changes. Total differentials can be generalized.
A continuous function not differentiable at the rationals but
The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. We can use this to approximate error propagation;. Total.
Differentiable Programming A Simple Introduction
Total differentials can be generalized. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). We can use this to approximate error propagation;. Let \(dx\), \(dy\) and \(dz\) represent changes. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted.
Differentiable Turbulence Paper and Code CatalyzeX
The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. We can use this to approximate error propagation;. The total differential gives an approximation of the change in z given small changes in x and y. Let \(dx\), \(dy\) and.
Total Differentials Can Be Generalized.
Let \(w=f(x,y,z)\) be continuous on an open set \(s\). For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. The total differential gives an approximation of the change in z given small changes in x and y. Let \(dx\), \(dy\) and \(dz\) represent changes.
We Can Use This To Approximate Error Propagation;.
The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted.