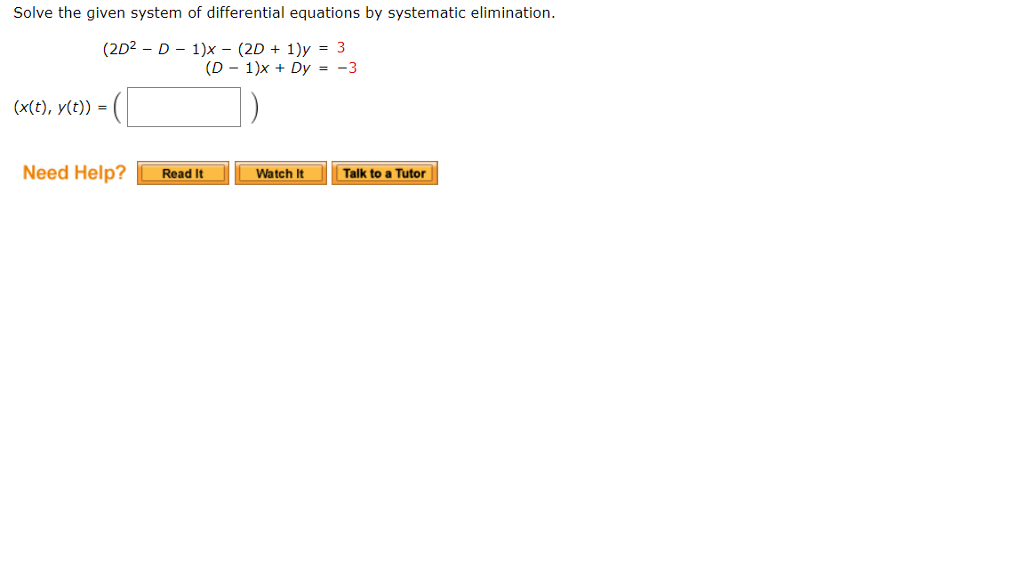
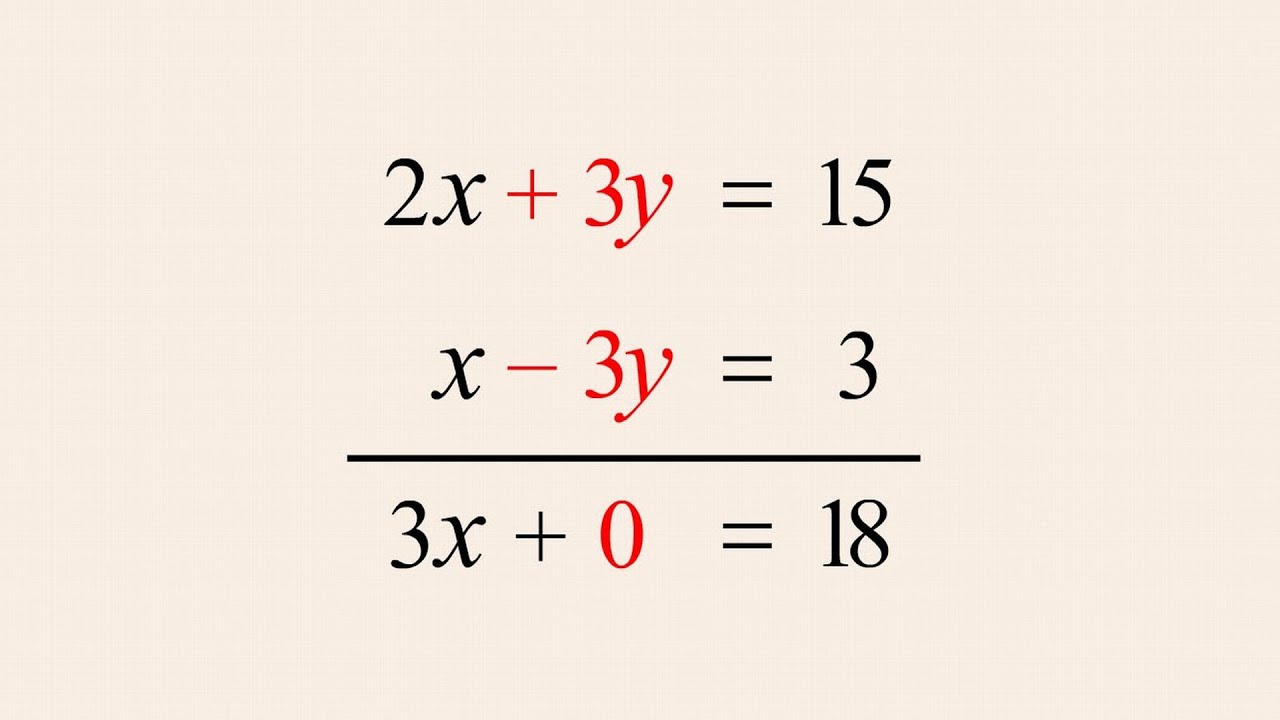Using Rref To Solve System Of Differential Equations - The system is consistent (i.e. The rref is a matrix that has. The following deals with finding all the solutions to a linear systems of. A = [1 1 5; B = [6 8 10 2]'; Create an augmented matrix that represents the system of equations. To solve the system, we form the augmented matrix and bring it to rref using row operations. Using a matrix and then row reducing into echelon form? Using rref on the augmented matrix yields: Use rref to solve the linear systems of equations.
B = [6 8 10 2]'; The system is consistent (i.e. Using a matrix and then row reducing into echelon form? There is no row in the final matrix that indicates that the system is. The rref is a matrix that has. To solve the system, we form the augmented matrix and bring it to rref using row operations. Using rref on the augmented matrix yields: A = [1 1 5; The following deals with finding all the solutions to a linear systems of. Create an augmented matrix that represents the system of equations.
To solve the system, we form the augmented matrix and bring it to rref using row operations. Create an augmented matrix that represents the system of equations. B = [6 8 10 2]'; The rref is a matrix that has. There is no row in the final matrix that indicates that the system is. Use rref to solve the linear systems of equations. I'm not sure how to set this up and solve it, to get the coefficients of the form. Using rref on the augmented matrix yields: The system is consistent (i.e. A = [1 1 5;
Solved Solve given systems of linear equations by converting
Use rref to solve the linear systems of equations. There is no row in the final matrix that indicates that the system is. The rref is a matrix that has. The following deals with finding all the solutions to a linear systems of. I'm not sure how to set this up and solve it, to get the coefficients of the.
Solved 2. Solve the following system of equations using rref
The following deals with finding all the solutions to a linear systems of. The rref is a matrix that has. Using rref on the augmented matrix yields: The system is consistent (i.e. B = [6 8 10 2]';
Solve System Of Equations Using Addition Method Calculator Mona
To solve the system, we form the augmented matrix and bring it to rref using row operations. There is no row in the final matrix that indicates that the system is. A = [1 1 5; Use rref to solve the linear systems of equations. Using rref on the augmented matrix yields:
Solved Solve systems of linear equations by converting them
Use rref to solve the linear systems of equations. There is no row in the final matrix that indicates that the system is. B = [6 8 10 2]'; The rref is a matrix that has. The following deals with finding all the solutions to a linear systems of.
Solved 1. Solve the system in two ways. Use rref and "\" to
Using a matrix and then row reducing into echelon form? Use rref to solve the linear systems of equations. The rref is a matrix that has. The following deals with finding all the solutions to a linear systems of. There is no row in the final matrix that indicates that the system is.
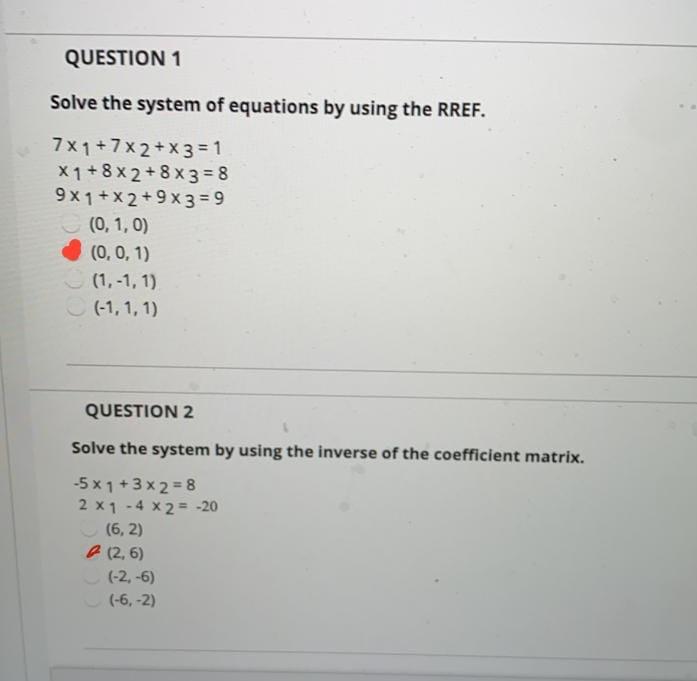
Solved Solve the system of equations by using the RREF.
The rref is a matrix that has. There is no row in the final matrix that indicates that the system is. Using rref on the augmented matrix yields: B = [6 8 10 2]'; To solve the system, we form the augmented matrix and bring it to rref using row operations.
Solved 3) Use RREF to solve the system of linear equations
The rref is a matrix that has. Using a matrix and then row reducing into echelon form? B = [6 8 10 2]'; To solve the system, we form the augmented matrix and bring it to rref using row operations. A = [1 1 5;
SOLVEDSolve the system of linear equations by using the rref command
A = [1 1 5; The following deals with finding all the solutions to a linear systems of. B = [6 8 10 2]'; Use rref to solve the linear systems of equations. The system is consistent (i.e.
Using Elimination To Solve Systems Of Equations Tessshebaylo
The rref is a matrix that has. Using a matrix and then row reducing into echelon form? Using rref on the augmented matrix yields: B = [6 8 10 2]'; Use rref to solve the linear systems of equations.
Solved Solve the given system of differential equations by
Using a matrix and then row reducing into echelon form? B = [6 8 10 2]'; I'm not sure how to set this up and solve it, to get the coefficients of the form. Using rref on the augmented matrix yields: The system is consistent (i.e.
To Solve The System, We Form The Augmented Matrix And Bring It To Rref Using Row Operations.
The rref is a matrix that has. Use rref to solve the linear systems of equations. The system is consistent (i.e. The following deals with finding all the solutions to a linear systems of.
B = [6 8 10 2]';
A = [1 1 5; I'm not sure how to set this up and solve it, to get the coefficients of the form. There is no row in the final matrix that indicates that the system is. Create an augmented matrix that represents the system of equations.
Using A Matrix And Then Row Reducing Into Echelon Form?
Using rref on the augmented matrix yields: