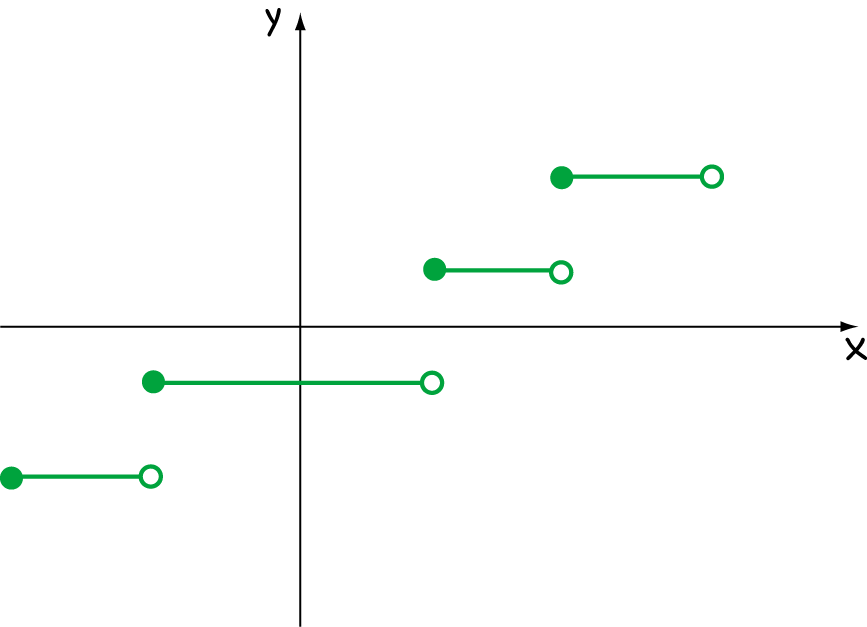
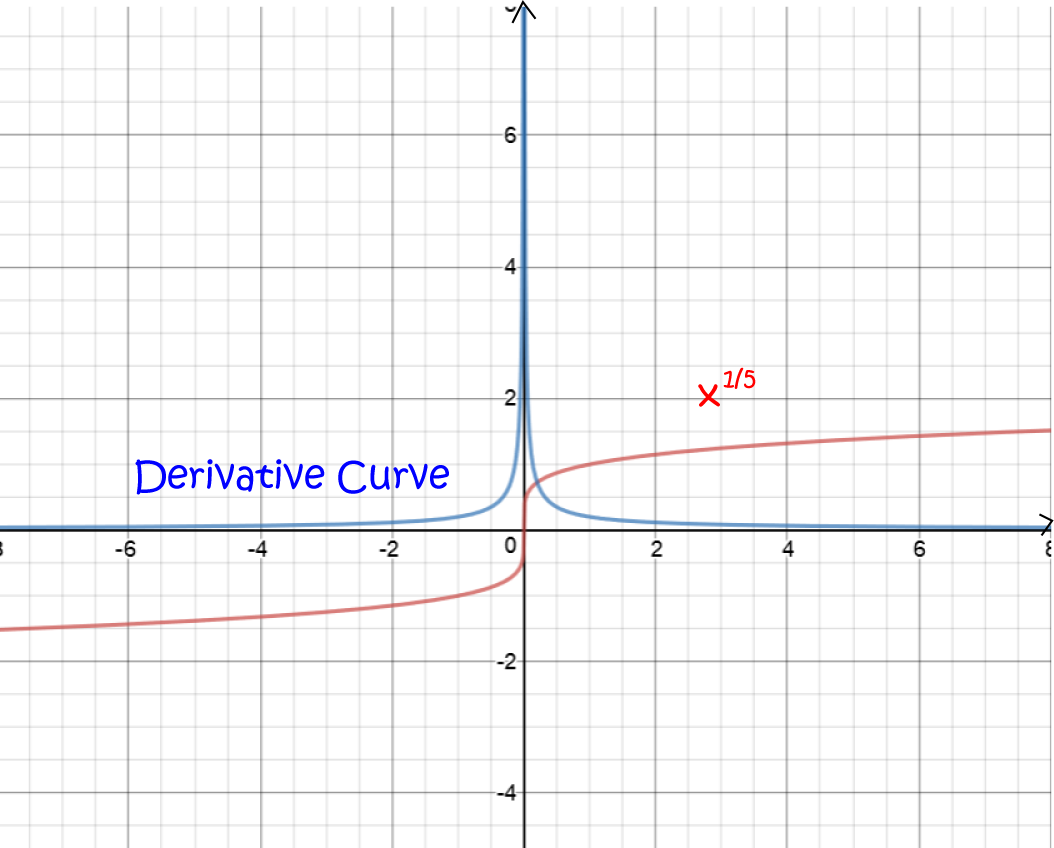
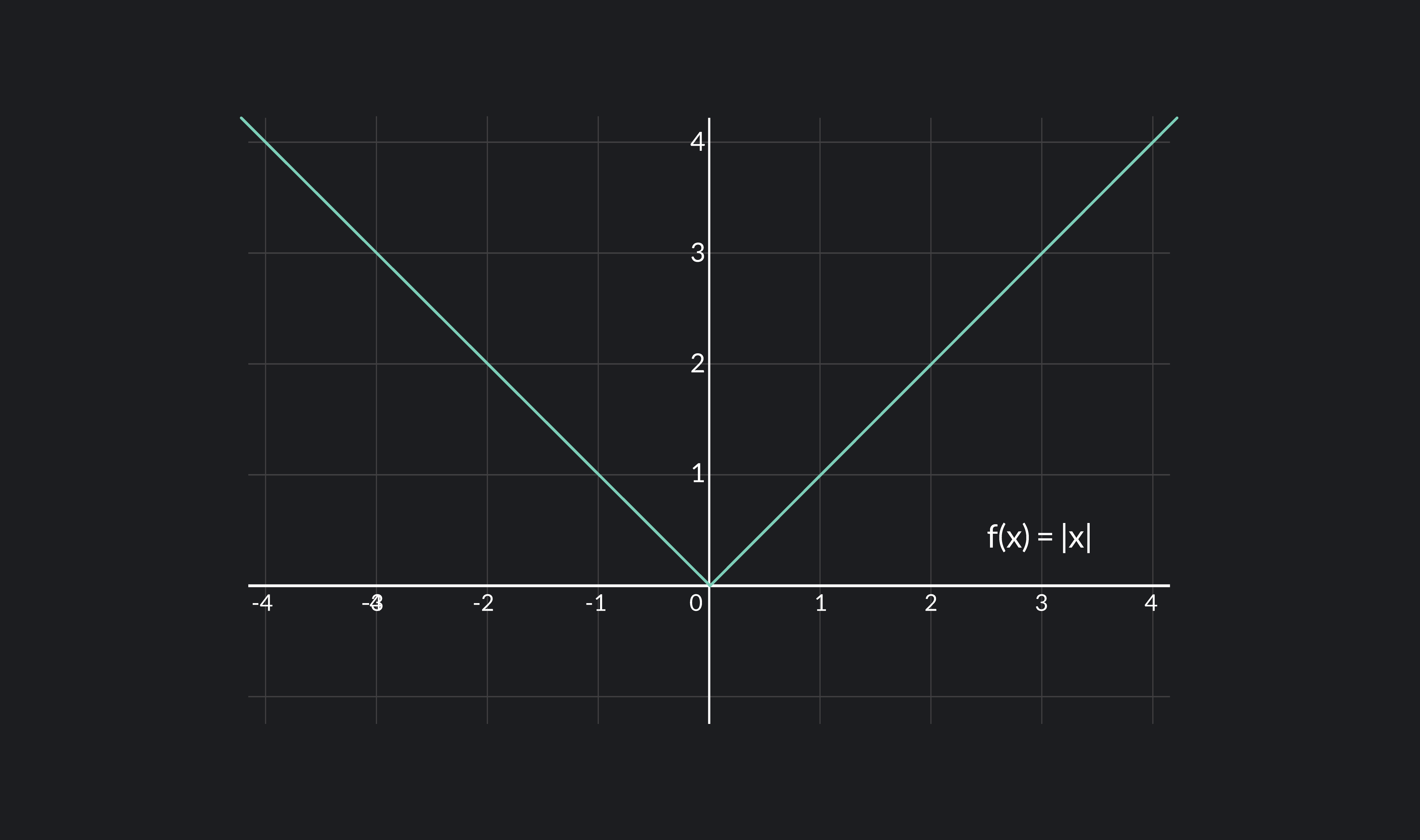
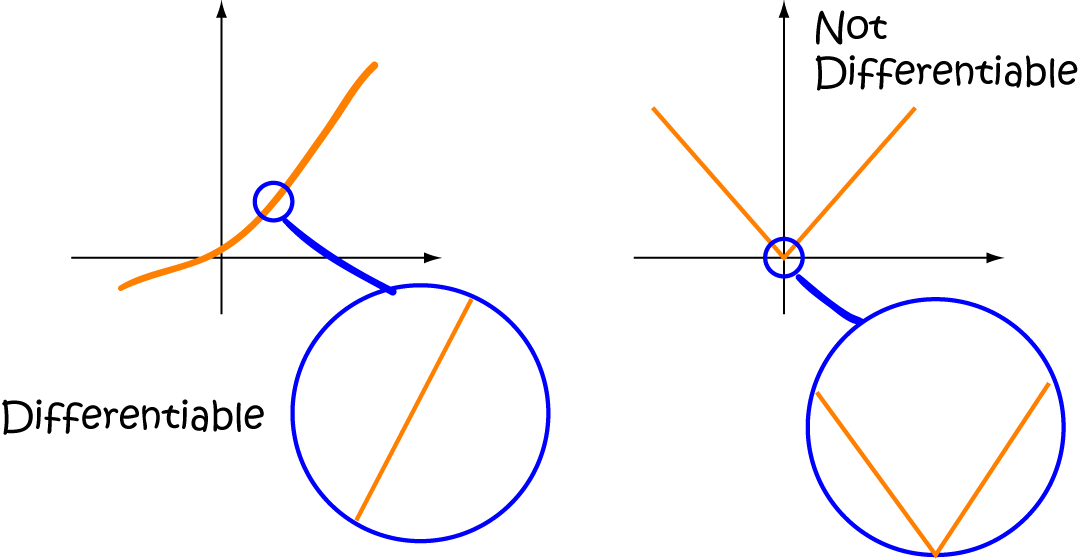
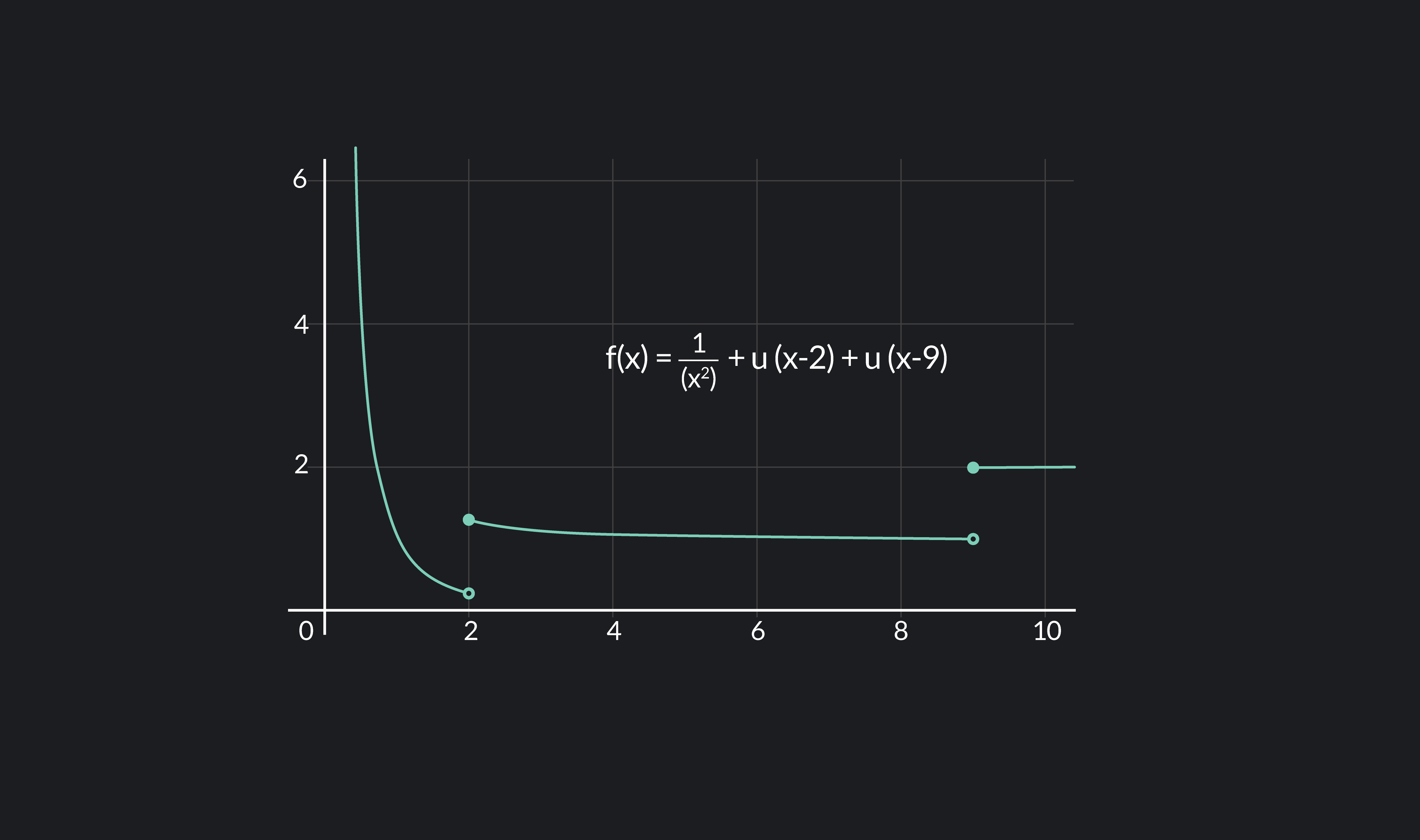
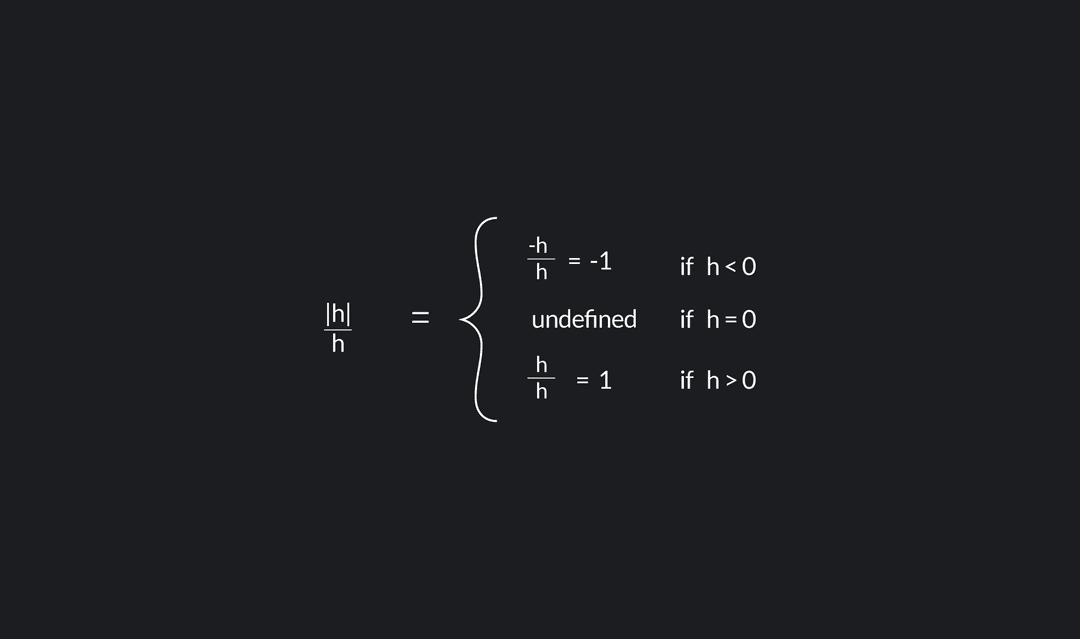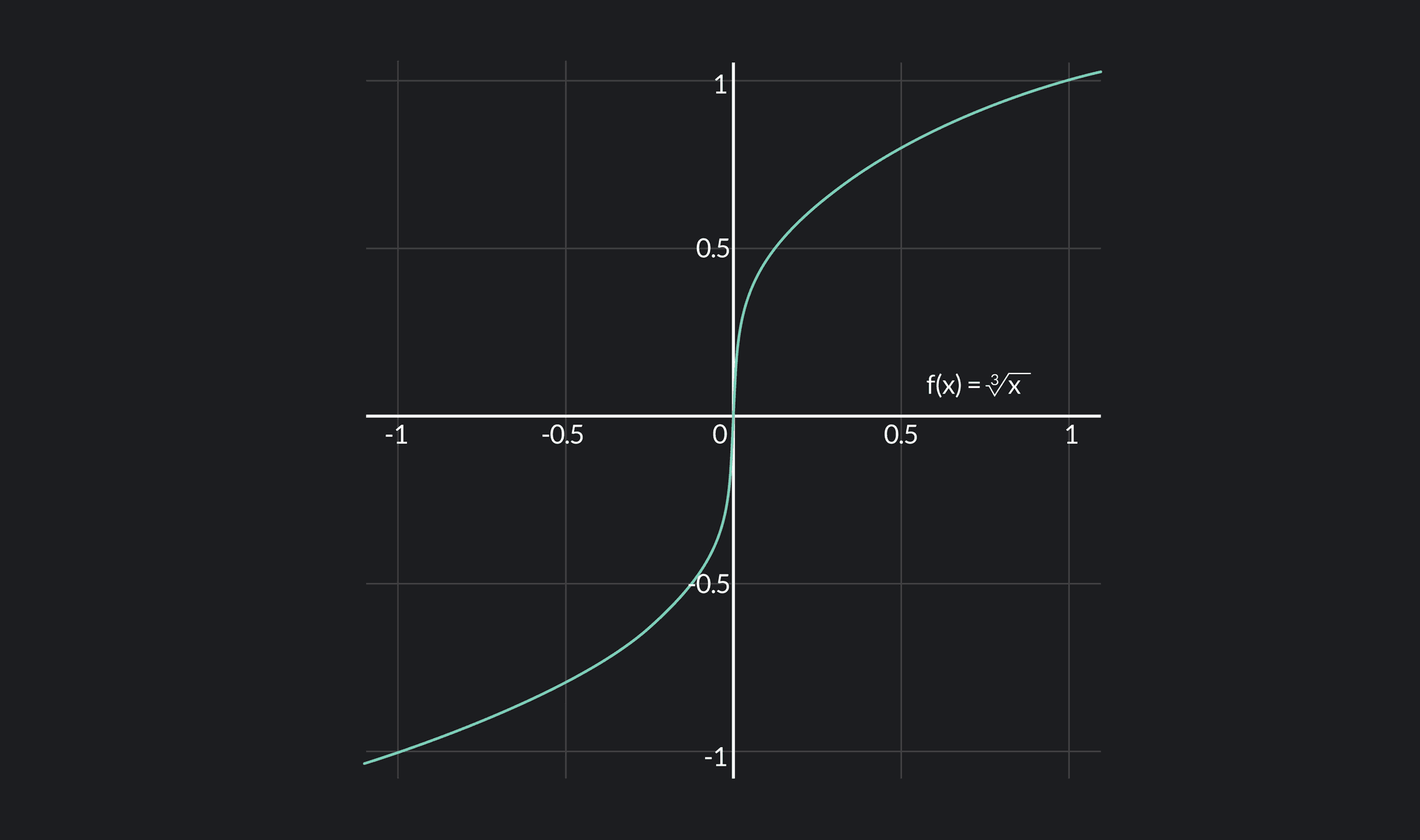What Does Differentiable In Calculus Mean - Use the total differential to approximate the change in a function of two. Let's have another look at our first example: Explain when a function of two variables is differentiable. That is, the graph of a. In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain.
Explain when a function of two variables is differentiable. In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. Use the total differential to approximate the change in a function of two. That is, the graph of a. Let's have another look at our first example:
Explain when a function of two variables is differentiable. Let's have another look at our first example: Use the total differential to approximate the change in a function of two. That is, the graph of a. In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain.
What does it mean for a function to be differentiable? Calculus
Let's have another look at our first example: In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. Use the total differential to approximate the change in a function of two. That is, the graph of a. Explain when a function of two variables is differentiable.
What does it mean for a function to be differentiable? Calculus
That is, the graph of a. Explain when a function of two variables is differentiable. Let's have another look at our first example: Use the total differential to approximate the change in a function of two. In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain.
Differentiable Function Meaning, Formulas and Examples Outlier
Explain when a function of two variables is differentiable. In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. That is, the graph of a. Use the total differential to approximate the change in a function of two. Let's have another look at our first example:
What does it mean for a function to be differentiable? Calculus
Explain when a function of two variables is differentiable. That is, the graph of a. Use the total differential to approximate the change in a function of two. In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. Let's have another look at our first example:
Differentiable Function Meaning, Formulas and Examples Outlier
That is, the graph of a. In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. Let's have another look at our first example: Use the total differential to approximate the change in a function of two. Explain when a function of two variables is differentiable.
What does it mean for a function to be differentiable? Calculus
Explain when a function of two variables is differentiable. Use the total differential to approximate the change in a function of two. That is, the graph of a. Let's have another look at our first example: In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain.
Differentiable Function Meaning, Formulas and Examples Outlier
In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. Let's have another look at our first example: Use the total differential to approximate the change in a function of two. That is, the graph of a. Explain when a function of two variables is differentiable.
Differentiable Function Meaning, Formulas and Examples Outlier
In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. That is, the graph of a. Use the total differential to approximate the change in a function of two. Explain when a function of two variables is differentiable. Let's have another look at our first example:
What does it mean for a function to be differentiable? Calculus
Use the total differential to approximate the change in a function of two. That is, the graph of a. In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. Let's have another look at our first example: Explain when a function of two variables is differentiable.
Differentiable Function Meaning, Formulas and Examples Outlier
Explain when a function of two variables is differentiable. Let's have another look at our first example: In calculus, a differentiable function is a continuous function whose derivative exists at all points on its domain. That is, the graph of a. Use the total differential to approximate the change in a function of two.
In Calculus, A Differentiable Function Is A Continuous Function Whose Derivative Exists At All Points On Its Domain.
That is, the graph of a. Use the total differential to approximate the change in a function of two. Let's have another look at our first example: Explain when a function of two variables is differentiable.