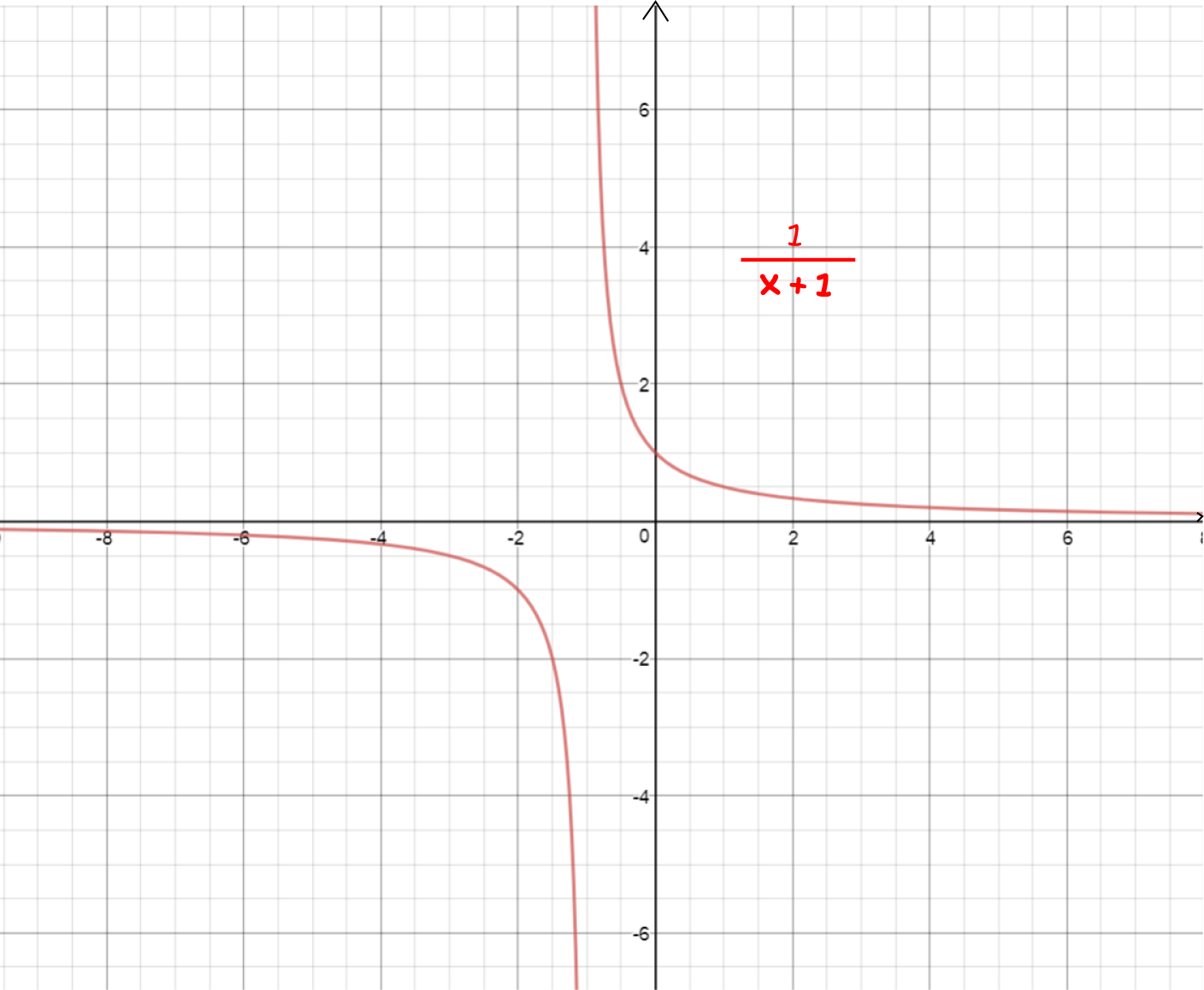
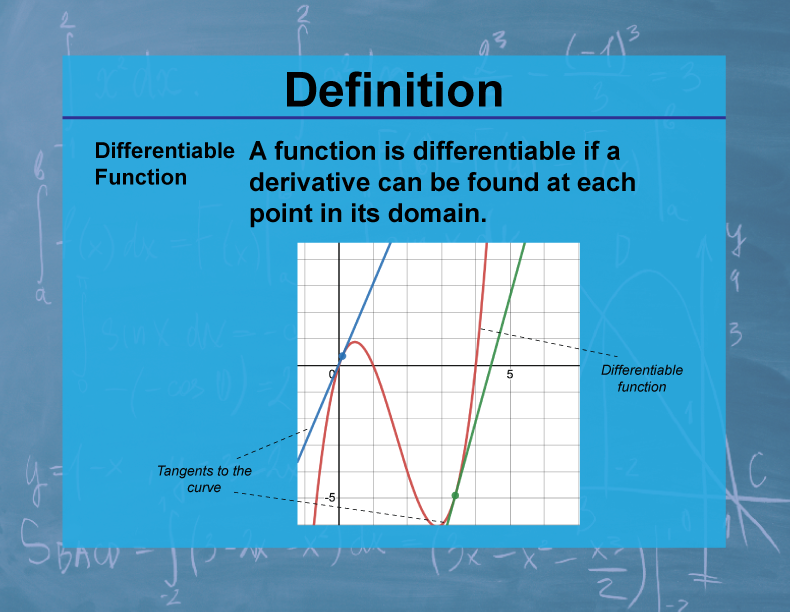
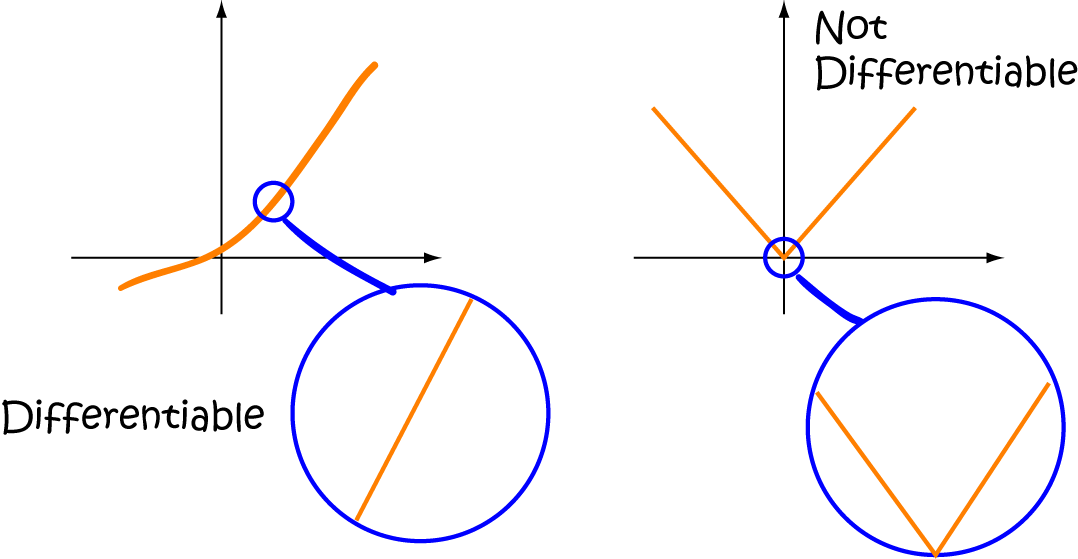
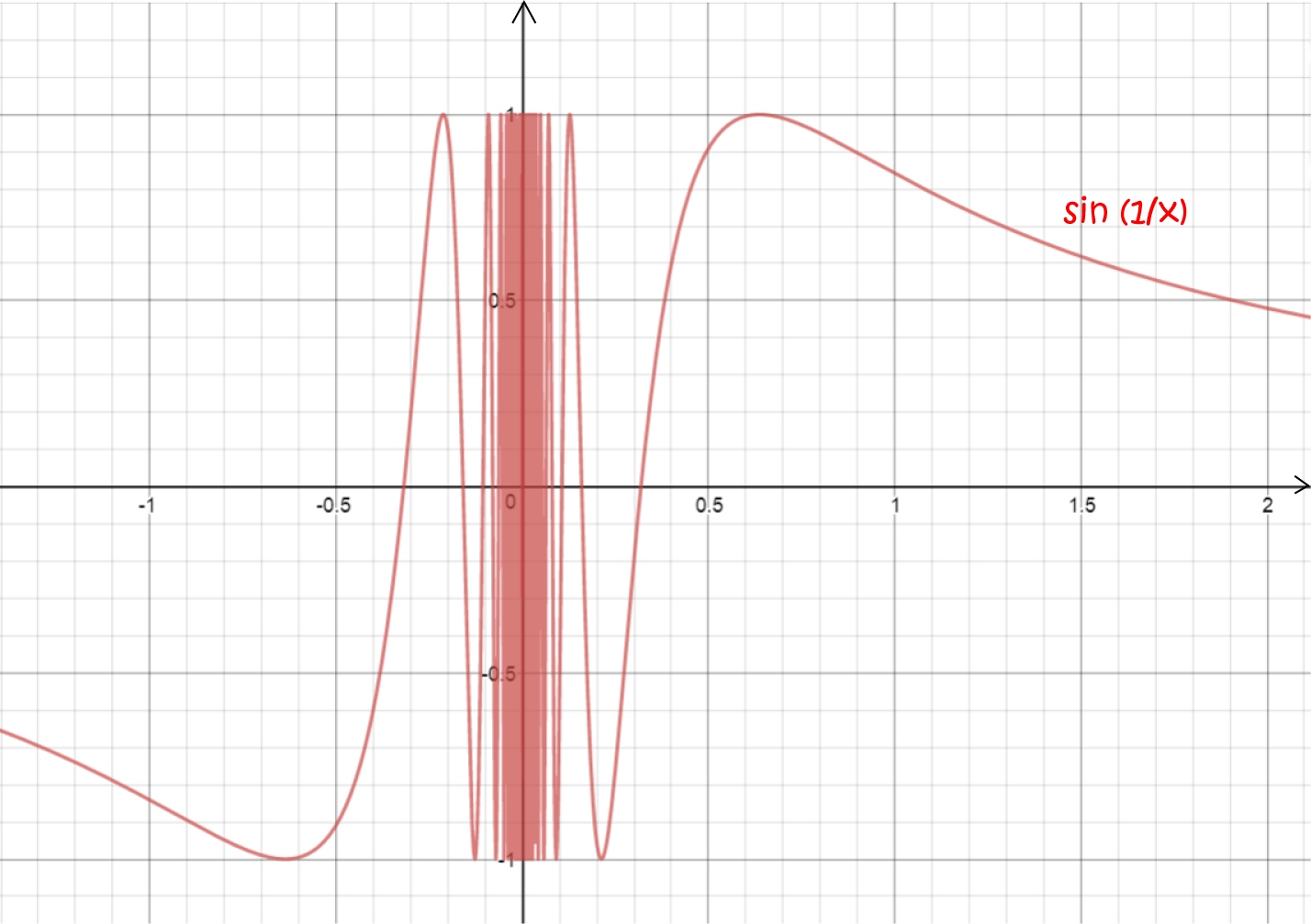
What Is Differentiable In Calculus - A function is deemed differentiable at a point if it. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. In calculus, differentiability lies at the heart of understanding smoothness in functions. Use the total differential to approximate the change in a function of two. Let's have another look at our first example: Explain when a function of two variables is differentiable.
Explain when a function of two variables is differentiable. Use the total differential to approximate the change in a function of two. In calculus, differentiability lies at the heart of understanding smoothness in functions. Let's have another look at our first example: A function is deemed differentiable at a point if it. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),.
Explain when a function of two variables is differentiable. Use the total differential to approximate the change in a function of two. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. In calculus, differentiability lies at the heart of understanding smoothness in functions. Let's have another look at our first example: A function is deemed differentiable at a point if it.
Differentiable vs. Continuous Functions Understanding the Distinctions
Let's have another look at our first example: In calculus, differentiability lies at the heart of understanding smoothness in functions. A function is deemed differentiable at a point if it. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. Explain when a function of two variables is differentiable.
What does it mean for a function to be differentiable? Calculus
\(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. A function is deemed differentiable at a point if it. In calculus, differentiability lies at the heart of understanding smoothness in functions. Let's have another look at our first example: Explain when a function of two variables is differentiable.
Differentiable function Wikiwand
\(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. In calculus, differentiability lies at the heart of understanding smoothness in functions. Use the total differential to approximate the change in a function of two. Explain when a function of two variables is differentiable. A function is deemed differentiable.
DefinitionCalculus TopicsDifferentiable Function Media4Math
\(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. Use the total differential to approximate the change in a function of two. Explain when a function of two variables is differentiable. A function is deemed differentiable at a point if it. In calculus, differentiability lies at the heart.
Differential Calculus Terms, Formulas, Rules, Examples
In calculus, differentiability lies at the heart of understanding smoothness in functions. A function is deemed differentiable at a point if it. Let's have another look at our first example: Use the total differential to approximate the change in a function of two. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if.
What does it mean for a function to be differentiable? Calculus
A function is deemed differentiable at a point if it. Explain when a function of two variables is differentiable. Use the total differential to approximate the change in a function of two. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. In calculus, differentiability lies at the heart.
What does it mean for a function to be differentiable? Calculus
Use the total differential to approximate the change in a function of two. Explain when a function of two variables is differentiable. In calculus, differentiability lies at the heart of understanding smoothness in functions. A function is deemed differentiable at a point if it. Let's have another look at our first example:
What does it mean for a function to be differentiable? Calculus
Explain when a function of two variables is differentiable. A function is deemed differentiable at a point if it. Use the total differential to approximate the change in a function of two. Let's have another look at our first example: In calculus, differentiability lies at the heart of understanding smoothness in functions.
What does it mean for a function to be differentiable? Calculus
A function is deemed differentiable at a point if it. Explain when a function of two variables is differentiable. In calculus, differentiability lies at the heart of understanding smoothness in functions. Use the total differential to approximate the change in a function of two. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that.
What does it mean for a function to be differentiable? Calculus
A function is deemed differentiable at a point if it. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. In calculus, differentiability lies at the heart of understanding smoothness in functions. Let's have another look at our first example: Explain when a function of two variables is differentiable.
Use The Total Differential To Approximate The Change In A Function Of Two.
A function is deemed differentiable at a point if it. Explain when a function of two variables is differentiable. \(f\) is differentiable at \((x_0,y_0)\) if, given \(\epsilon >0\), there is a \(\delta >0\) such that if \(||\langle dx,dy\rangle|| < \delta\),. In calculus, differentiability lies at the heart of understanding smoothness in functions.