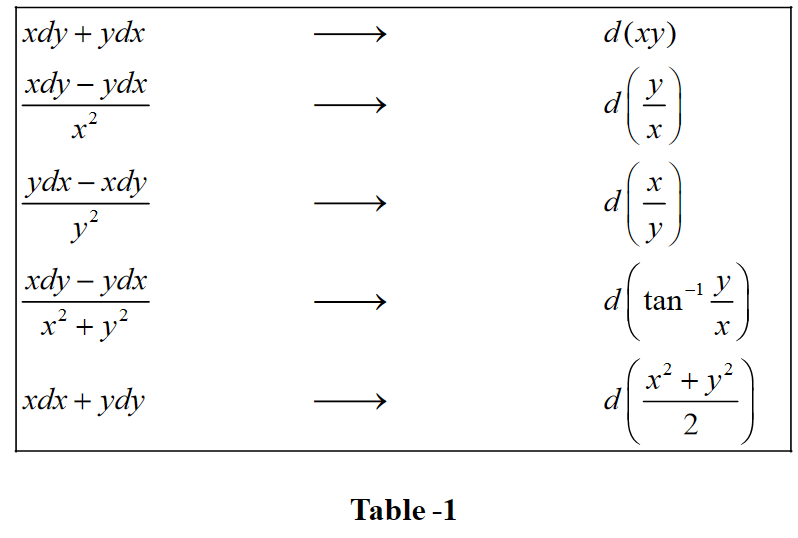
Exact Differential Equations - Is said to be exact. If you have had vector calculus , this is the same as finding the potential functions. This is why such a differential equation is called an exact differential equation. A differential equation with a potential function is called exact. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. From the previous example, a potential function for the differential. This means that a function u(x,y) exists such that:.
This means that a function u(x,y) exists such that:. A differential equation with a potential function is called exact. Is said to be exact. If you have had vector calculus , this is the same as finding the potential functions. This is why such a differential equation is called an exact differential equation. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. From the previous example, a potential function for the differential.
P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. If you have had vector calculus , this is the same as finding the potential functions. A differential equation with a potential function is called exact. Is said to be exact. This means that a function u(x,y) exists such that:. From the previous example, a potential function for the differential. This is why such a differential equation is called an exact differential equation.
Exact Differential Equations PDF Differential Equations Equations
This is why such a differential equation is called an exact differential equation. If you have had vector calculus , this is the same as finding the potential functions. From the previous example, a potential function for the differential. A differential equation with a potential function is called exact. This means that a function u(x,y) exists such that:.
Exact differential equations Yawin
Is said to be exact. A differential equation with a potential function is called exact. From the previous example, a potential function for the differential. This means that a function u(x,y) exists such that:. If you have had vector calculus , this is the same as finding the potential functions.
[Solved] SOLVE THE FOLLOWING EXACT DIFFERENTIAL EQUATIONS SOLVE THE
A differential equation with a potential function is called exact. This is why such a differential equation is called an exact differential equation. Is said to be exact. If you have had vector calculus , this is the same as finding the potential functions. This means that a function u(x,y) exists such that:.
Exact Differential Equations Differential Equations Equations
If you have had vector calculus , this is the same as finding the potential functions. This is why such a differential equation is called an exact differential equation. A differential equation with a potential function is called exact. Is said to be exact. This means that a function u(x,y) exists such that:.
LECTURE 5 Exact Differential Equations PDF Equations Fair Use
P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This means that a function u(x,y) exists such that:. This is why such a differential equation is called an exact differential equation. Is said to be exact. From the previous example, a potential function for the differential.
Exact differential equations
Is said to be exact. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. From the previous example, a potential function for the differential. This is why such a differential equation is called an exact differential equation. A differential equation with a potential function is called exact.
Examples On Exact Differential Equations What is Examples On Exact
Is said to be exact. A differential equation with a potential function is called exact. This means that a function u(x,y) exists such that:. This is why such a differential equation is called an exact differential equation. From the previous example, a potential function for the differential.
[Solved] SOLVE THE FOLLOWING EXACT DIFFERENTIAL EQUATIONS SOLVE THE
A differential equation with a potential function is called exact. If you have had vector calculus , this is the same as finding the potential functions. From the previous example, a potential function for the differential. This is why such a differential equation is called an exact differential equation. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the.
[Solved] Determine Whether The Following Differential Equations Are
This is why such a differential equation is called an exact differential equation. This means that a function u(x,y) exists such that:. If you have had vector calculus , this is the same as finding the potential functions. Is said to be exact. From the previous example, a potential function for the differential.
Differential Equations Owlcation
P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This is why such a differential equation is called an exact differential equation. From the previous example, a potential function for the differential. This means that a function u(x,y) exists such that:. A differential equation with a potential function is called exact.
A Differential Equation With A Potential Function Is Called Exact.
This is why such a differential equation is called an exact differential equation. From the previous example, a potential function for the differential. Is said to be exact. If you have had vector calculus , this is the same as finding the potential functions.
P(X,Y)Dx+Q(X,Y)Dy = 0 If ∂P ∂Y = ∂Q ∂X Then The O.de.
This means that a function u(x,y) exists such that:.