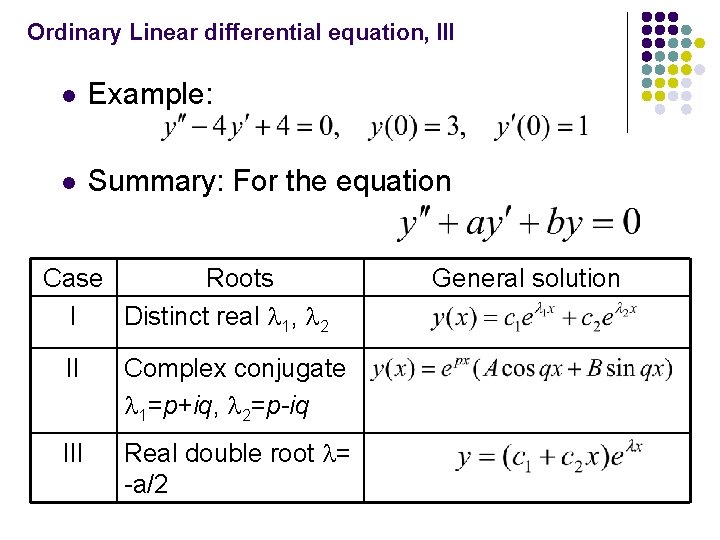
Explicit Solution Differential Equations - Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1. Explicit solution is a solution where the dependent variable can be separated. Basic theory of linear differential. Order and linear vs nonlinear of a de. Introduction to differential equations important topics in this chapter: If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say it is an explicit solution to the equation. For example, $x+2y=0$ is explicit because if y is.
Order and linear vs nonlinear of a de. If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say it is an explicit solution to the equation. Introduction to differential equations important topics in this chapter: For example, $x+2y=0$ is explicit because if y is. Basic theory of linear differential. Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1. Explicit solution is a solution where the dependent variable can be separated.
Order and linear vs nonlinear of a de. For example, $x+2y=0$ is explicit because if y is. Basic theory of linear differential. Introduction to differential equations important topics in this chapter: Explicit solution is a solution where the dependent variable can be separated. Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1. If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say it is an explicit solution to the equation.
[Solved] Find the general solution of the following differential
Introduction to differential equations important topics in this chapter: Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1. Basic theory of linear differential. Explicit solution is a solution where the dependent variable can be separated. If a function (x) is substituted for y in a de and satis es the equation.
Solved 1. Find explicit solutions to the following
If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say it is an explicit solution to the equation. Explicit solution is a solution where the dependent variable can be separated. For example, $x+2y=0$ is explicit because if y is. Introduction to differential equations important topics.
Differential Equations Ordinary differential equation ODE Partial
Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1. If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say it is an explicit solution to the equation. Basic theory of linear differential. For example, $x+2y=0$ is.
Solved Solve the following differential equations. (Explicit
If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say it is an explicit solution to the equation. For example, $x+2y=0$ is explicit because if y is. Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1..
Find the explicit particular solution of the differenti... Math
Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1. Introduction to differential equations important topics in this chapter: Explicit solution is a solution where the dependent variable can be separated. Basic theory of linear differential. If a function (x) is substituted for y in a de and satis es the equation.
First Order Differential Equation Worksheet Equations Worksheets
If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say it is an explicit solution to the equation. Order and linear vs nonlinear of a de. For example, $x+2y=0$ is explicit because if y is. Math 2233 (differential equations) lecture 2 section 1.2 solutions and.
[Solved] SOLVE THE FOLLOWING EXACT DIFFERENTIAL EQUATIONS SOLVE THE
If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say it is an explicit solution to the equation. Introduction to differential equations important topics in this chapter: Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1..
Ordinary Differential Equations (A Comprehensive Resource)
Explicit solution is a solution where the dependent variable can be separated. For example, $x+2y=0$ is explicit because if y is. Order and linear vs nonlinear of a de. Introduction to differential equations important topics in this chapter: If a function (x) is substituted for y in a de and satis es the equation for all x in some interval.
Solved Find A General Solution To The Following Different...
Explicit solution is a solution where the dependent variable can be separated. Basic theory of linear differential. Introduction to differential equations important topics in this chapter: For example, $x+2y=0$ is explicit because if y is. If a function (x) is substituted for y in a de and satis es the equation for all x in some interval i, we say.
Differential Equations Ordinary differential equation ODE Partial
Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1. Basic theory of linear differential. Order and linear vs nonlinear of a de. For example, $x+2y=0$ is explicit because if y is. Introduction to differential equations important topics in this chapter:
Basic Theory Of Linear Differential.
Math 2233 (differential equations) lecture 2 section 1.2 solutions and initial value problems goal of this section 1. Explicit solution is a solution where the dependent variable can be separated. Introduction to differential equations important topics in this chapter: Order and linear vs nonlinear of a de.
If A Function (X) Is Substituted For Y In A De And Satis Es The Equation For All X In Some Interval I, We Say It Is An Explicit Solution To The Equation.
For example, $x+2y=0$ is explicit because if y is.