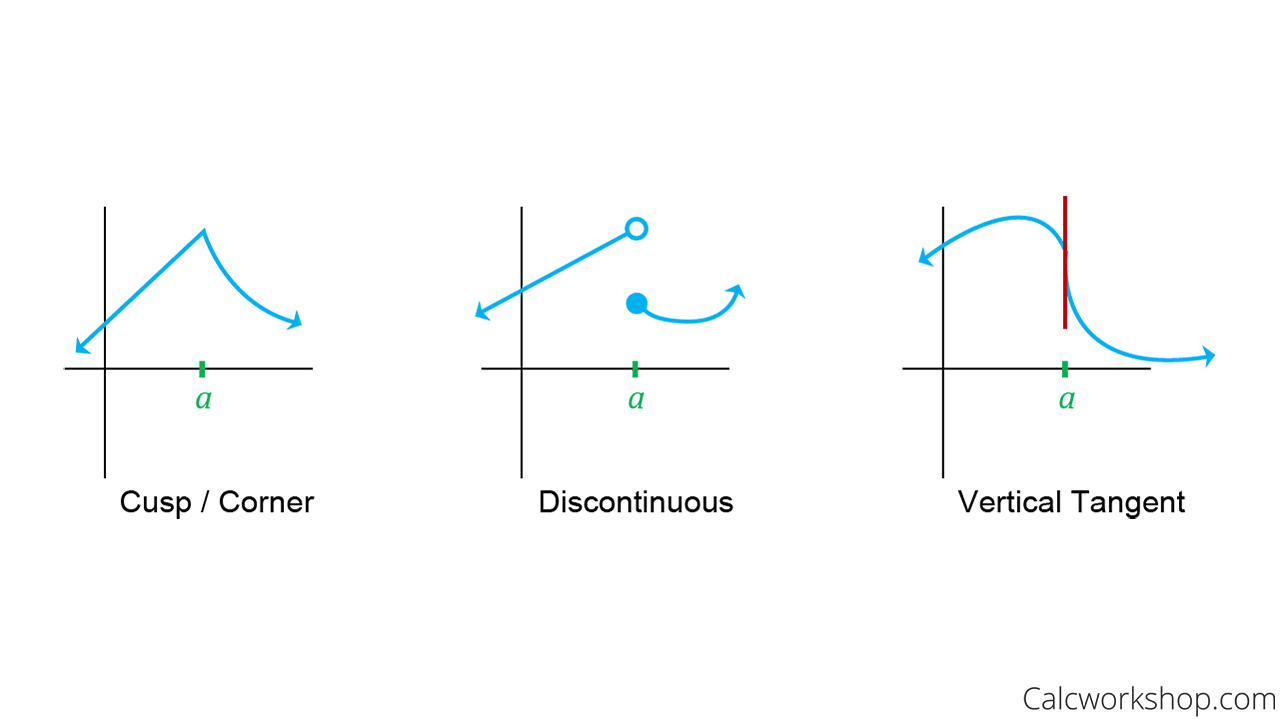
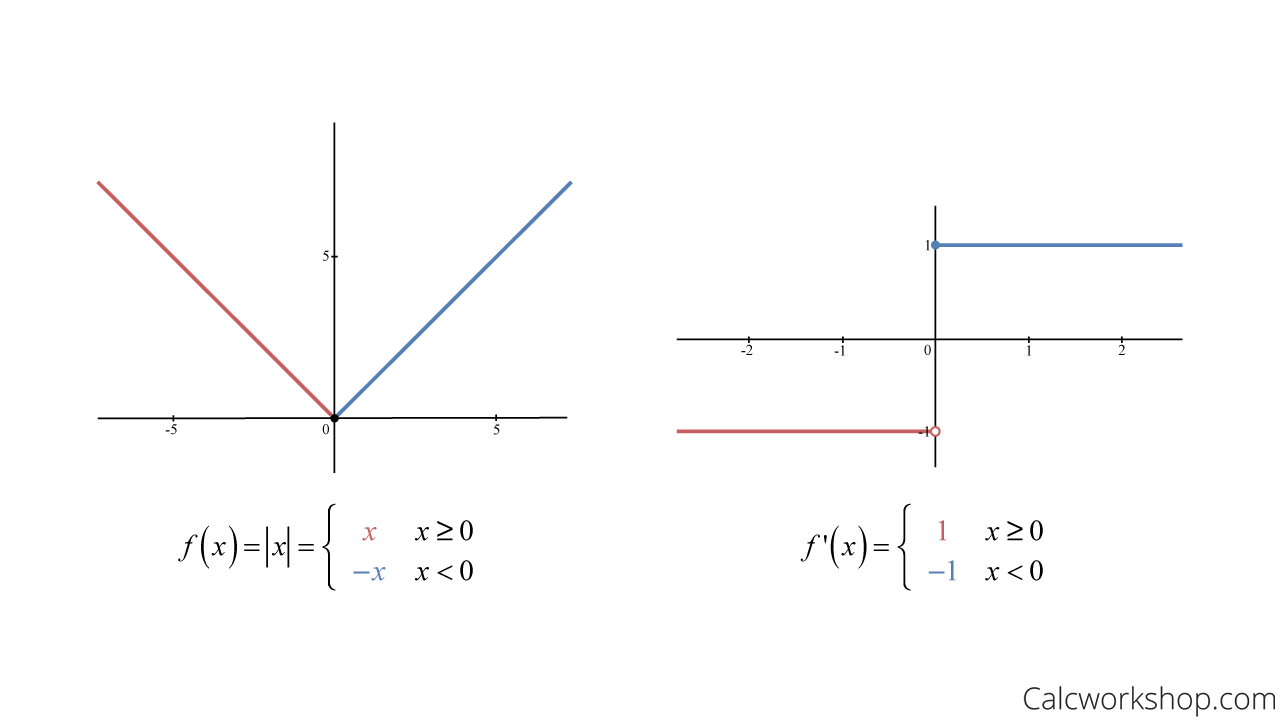
How To Determine Differentiability - We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Solved Determine the relationship between differentiability and
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Continuity and Differentiability (Fully Explained w/ Examples!)
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Continuity and Differentiability (Fully Explained w/ Examples!)
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Continuity and Differentiability (Fully Explained w/ Examples!)
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
SOLUTION Calculus Differentiability Presentation Studypool
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Continuity and Differentiability (Fully Explained w/ Examples!)
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
derivatives Differentiability Implies Continuity (Multivariable
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Solved Determine the relationship between differentiability and
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Continuity and Differentiability (Fully Explained w/ Examples!)
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Worksheet 6 Continuity Differentiability PDF Function (Mathematics
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.